- 导数的几何意义
- 共149题
已知函数
(1)求函数
(2)若函数
(3)若函数

正确答案
见解析。
解析
(1)

所以



(2) 由题意




由












又
综上,若函数

(3) 由题意,


若




则






综上,若函数

知识点
若曲线



正确答案
2
解析
求导得









知识点
已知正数



正确答案
解析
略
知识点
定义在区间










正确答案
①④
解析
略
知识点
已知存在实数a,满足对任意的实数b,直线y=-x+b都不是曲线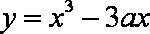
正确答案
解析
直线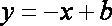
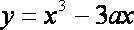
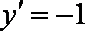
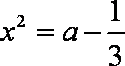
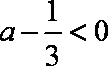
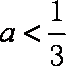
知识点
已知曲线

正确答案
-1
解析
f ′(x)=(n+1)xn,k=f ′(1)=n+1,点P(1,1)处的切线方程为:y-1=(n+1)(x-1),令y=0得,x=1-=,即xn=,∴x1×x2×…×x2011=×××…×


知识点
设函数







(1)写出
(2)问:
(3)设

正确答案
见解析
解析
解析:(1)、因为函数

所以
函数

(2)设
直线
则

联立






(3)


∴

∴ 

当且仅当
∴


知识点
设函数
(1)当b>

(2)求函数
正确答案
(1)单调递增,
(2)








解析
(1)函数


令








即当


(2)分以下几种情形讨论:由(1)知当

(2)当






(3)当



当


此时


当




此时

综上可知,









知识点
若函数


正确答案
解析
眼睛看到这个是三次函数,头脑中就闪现一般解题办法,求导解三次。这就是转化一念间
第一步识别条件: 继续识别条件:
第二步转化条件: 求导,把范围代入,看看导数的范围是啥,求出来的这个是切线的斜率。
第三步看问定向:倾斜角为
行了,画个正切函数图像,
知识点
若函数


正确答案
解析
眼睛看到这个是三次函数,头脑中就闪现一般解题办法,求导解三次。这就是转化一念间
第一步识别条件: 继续识别条件:
第二步转化条件: 求导,把范围代入,看看导数的范围是啥,求出来的这个是切线的斜率。
第三步看问定向: 倾斜角为
行了,画个正切函数图像,
第四步结论已出现:对照着找找角就行了
知识点
扫码查看完整答案与解析