导数的运算
共219题

· 导数的运算

导数的运算
共219题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：填空题

填空题 · 20 分

请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。

正确答案

测试

题型：单选题

单选题 · 5 分

根据右边框图，对大于2的整数，输出数列的通项公式是（）

正确答案

解析

知识点

导数的运算

题型：简答题

简答题 · 14 分

已知函数

（1）设函数，求的单调区间与极值；

（2）设，解关于的方程

（3）试比较与的大小。

正确答案

见解析

解析

（1）由，（≥）知，

，令，得

当时，；当时，；

故当时，单调递减；

当时，单调递增；

所以是其极小值点，且极小值为。

（2）因为,故原方程可化为；

即

等价于:

故画出函数图象后,由方程与函数的思想,讨论得:

1当时,原方程有一解;

2当时,原方程有两解;

3当时,原方程有一解;

4当时,原方程无解。

（3）由已知得。

设数列的前项和为，且，。

从而有，

当时，，

又

则对任意的，有。

又因为，所以，故。

知识点

导数的运算

题型：单选题

单选题 · 5 分

设曲线y＝ax－ln(x＋1)在点(0，0)处的切线方程为y＝2x，则a＝(　　)

正确答案

解析

知识点

导数的几何意义导数的运算

题型：单选题

单选题 · 5 分

已知是抛物线的焦点，点，在该抛物线上且位于轴的两侧，（其中为坐标原点），则与面积之和的最小值是

正确答案

解析

设直线AB的方程为：，点，，又，直线AB与轴的交点（不妨假设）

由，所以

又

因为点，在该抛物线上且位于轴的两侧，所以，故

于是

当且仅当时取“”

所以与面积之和的最小值是

知识点

导数的运算

题型：简答题

简答题 · 13 分

工作人员需进入核电站完成某项具有高辐射危险的任务，每次只派一个人进去，且每个人只派一次，工作时间不超过10分钟。如果前一个人10分钟内不能完成任务则撤出，再派下一个人，现在一共只有甲、乙、丙三个人可派，他们各自能完成任务的概率分别为，假设互不相等，且假定各人能否完成任务的事件相互独立。

（1）如果按甲最先、乙次之、丙最后的顺序派人，求任务能被完成的概率。若改变三个人被派出的先后顺序，任务能被完成的概率是否发生变化？

（2）若按某指定顺序派人，这三个人各自能完成任务的概率依次为，其中是的一个排列，求所需派出人员数目X的分布列和均值（数学期望）EX；

（3）假定，试分析以怎样的先后顺序派出人员，可使所需派出的人员数目的均值（数学期望）达到最小。

正确答案

见解析

解析

（1）无论以怎样的顺序派出人员，任务不能被完成的概率都是，所以任务能被完成的概率与三个人被派出的先后顺序无关，并等于

（2）当依次派出的三个人各自完成任务的概率分别为时，随机变量X的分布列为

所需派出的人员数目的均值（数学期望）EX是

EX=++

（3）（方法一）由（2）的结论知，当甲最先、乙次之、丙最后的顺序派人时，

EX=

根据常理，优先派出完成任务概率大的人，可减少所需派出的人员数目的均值。

下面证明：对于的任意排列，都有

（＊）

事实上，

即（＊）成立。

（方法二）（ⅰ）可将（2）中所求的EX改写为，若交换前两人的派出顺序，则变为。由此可见，当时，交换前两人的派出顺序可减少均值。

（ⅱ）也可将（2）中所求的EX改写为，若交换后两人的派出顺序，则变为。由此可见，若保持第一个派出的人选不变，当时，交换后两人的派出顺序也可减少均值。

综合（ⅰ）（ⅱ）可知，当=时，EX达到最小。即完成任务概率大的人优先派出，可减少所需派出人员数目的均值，这一结论是合乎常理的

知识点

导数的运算

题型：简答题

简答题 · 13 分

设的导数满足其中常数.

（1）求曲线在点处的切线方程。

（2）设求函数的极值。

正确答案

（1）

（2）

解析

（1）因，故，

令，得，由已知，解得

又令，得，由已知，解得

因此，从而

又因为，故曲线在点处的切线方程为，即

（2）由（1）知，，从而有，

令，解得。

当时，，故在为减函数，

当时，，故在为增函数，

当时，，故在为减函数，

从而函数在处取得极小值，在出取得极大值

知识点

导数的几何意义导数的运算

题型：单选题

单选题 · 5 分

若,则的解集为 ( )

A(0,)

B(-1,0)(2,)

C(2,)

D(-1,0)

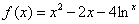
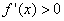
正确答案

解析

知识点

导数的运算

继续学习学习下一知识点

下一知识点 : 导数的加法与减法法则

百度题库 > 高考 > 理科数学 > 导数的运算

扫码查看完整答案与解析