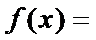- 导数的几何意义
- 共149题
若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b= 。
正确答案
知识点
设直线l1,l2分别是函数f(x)= 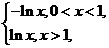
正确答案
知识点
15.已知f(x)为偶函数,当

正确答案
知识点
已知函数
24.设


25. 若对于任意


26.若



正确答案
解析



则



考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析
由题意得
令


此时

∵


因此实数

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析


由




而


因此







则




① 若








因此









则
② 若



可得
由
因此
因此


因此

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
已知函数
24.证明:当
25.证明:当

26.确定k的所以可能取值,使得存在


正确答案
(Ⅰ)详见解析
解析
解法一:(1)令
当



故当



考查方向
解题思路
求导,然后分类讨论求单调性
易错点
导数和函数的关系掌握不牢,不会利用导数判断函数的单调性
正确答案
(Ⅱ)详见解析
解析
(2)令

当



故对任意正实数
当


取






综上,当



考查方向
解题思路
先构造函数,然后求导判断单调区间,利用函数的单调性证明不等式。
易错点
不会构造函数,不会建立函数与导数之间的联系
正确答案
(Ⅲ) 
解析
(3)当



令
则有
故当





当



此时
令
则有
故当



故




则当
当

令
当




故当

综上,
考查方向
解题思路
分K大于1.K小于1和K等于1把不等式的左边去掉绝对值,然后再进行分类讨论,可得答案。
易错点
计算能力弱,求导分类讨论或重或漏
16.若直线y=kx+b是曲线y=lnx+2的切线,也是曲线y=ln(x+1)的切线,则b= 。
正确答案
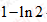
知识点
设函数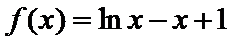
25.讨论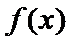
26.证明当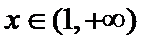
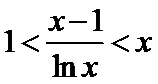
27.设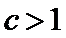
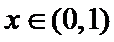
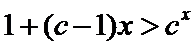
正确答案
(Ⅰ)当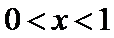
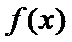
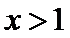
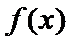
解析
(I)由题设,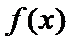
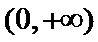
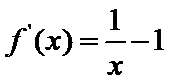
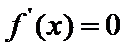
当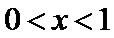
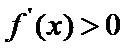
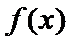
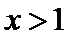
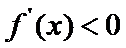
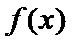
考查方向
解题思路
(I)首先求出导函数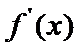
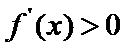
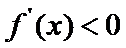
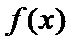
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅱ)(II)由(I)知,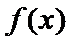
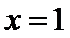
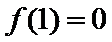
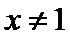
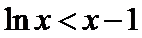
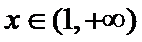
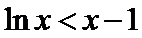
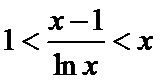
解析
(II)由(I)知,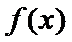
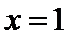
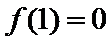
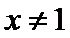
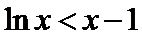
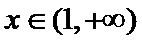
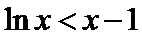
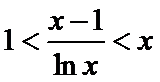
考查方向
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的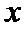

易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅲ)(III)由题设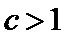
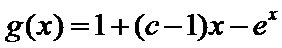
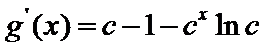
解得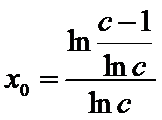
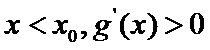
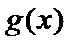
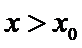
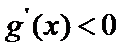
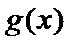
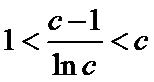
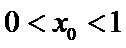
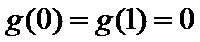
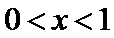
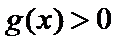
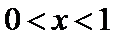
解析
(III)由题设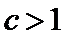
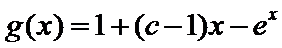
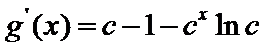
解得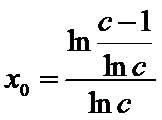
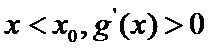
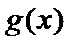
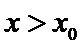
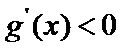
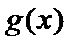
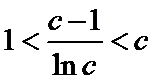
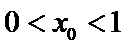
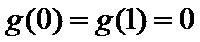
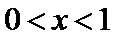
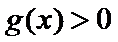
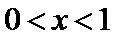
考查方向
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
(本小题满分13分)
已知函数
(Ⅰ)求函数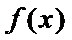
(Ⅱ)当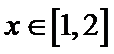
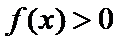
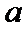
(Ⅲ)试问过点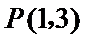
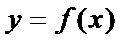
正确答案
考查方向
易错点
1、第一问在对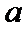
知识点
18.已知函数


(Ⅰ)如果函数





(Ⅱ)如果曲线


正确答案
(Ⅰ)

(Ⅱ)

解析
试题分析:本题属于导数的应用的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求,(2)要注意作差构造新函数
(Ⅰ)解:求导,得


由题意,得切线l的斜率


又切点坐标为

(Ⅱ)解:设函数

“曲线


个零点”.
求导,得
① 当
由



又因为


②当
当


所以


所以当

故

③ 当
令

当


所以


所以当

因为



所以
又因为存在

所以存在

所以函数

综上,曲线



考查方向
本题主要考查了导数的几何意义、利用导数研究函数的零点,导数作为一种工具,其应用主要分以下几类:
1.利用导数研究函数的单调性,
2.利用导数研究函数的极值、最值,
3.利用导数研究函数的零点个数,
4.利用导数研究不等式恒成立问题.
解题思路
本题考查导数的几何意义、导数在研究函数的应用,解题步骤如下:
1.求导,利用导数的几何意义得到等式,求出
2.作差构造函数,将问题转化为函数有且只有一个零点;
3.求导,通过导函数的符号研究函数的单调性与极值;
4.通过研究极值的符号得到答案.
易错点
忽视新函数的定义域
知识点
21.已知函数




(Ⅰ)求

(Ⅱ)证明:当

(Ⅲ)证明:对任意给定的正数



正确答案
(Ⅰ)见解析
(Ⅱ)见解析
(Ⅲ)见解析
解析
(Ⅰ)解,由

因为

所以

令

当



所以当


(Ⅱ)证明,令

由(Ⅰ)得

所以当


(Ⅲ)证明一,①若

由(Ⅱ)知,当



取


②若

要使不等式

而要使


令

所以当


取


又
易知
所以



综上,对任意给定的正数



证明二,对任意给定的正数

由(Ⅱ)知,当


当

因此,对任意给定的正数



证明三,首先证明当

令

由(Ⅱ)知,当

从而


所以

取


因此,对任意给定的正数



考查方向
解题思路
易错点
第一问建议做出极值表便于观察,防止出错;
第二问忽略证明第一问时得到的结论。
知识点
扫码查看完整答案与解析