导数的几何意义
共149题

· 导数的几何意义

导数的几何意义
共149题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln（x+1）的切线，则b= 。

正确答案

知识点

导数的几何意义

题型：填空题

填空题 · 5 分

16.若直线y=kx+b是曲线y=lnx+2的切线，也是曲线y=ln（x+1）的切线，则b= 。

正确答案

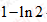
知识点

导数的几何意义

题型：单选题

单选题 · 13 分

（本小题满分13分）

已知函数．

（Ⅰ）求函数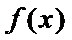的单调区间；

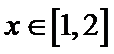
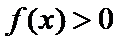
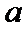
（Ⅱ）当时，都有成立，求的取值范围；

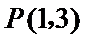
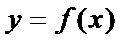
（Ⅲ）试问过点可作多少条直线与曲线相切？并说明理由．

正确答案

考查方向

本题考查了利用导数研究 “过点问题”的切线方程求法，考查了导数综合运用中的“恒成立问题”，还考查了分类讨论、数形结合等数学思想方法的灵活应用，意在训练考生的运算能力，分析问题和解决问题的能力，较难。

易错点

1、第一问在对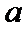分类讨论求单调区间时由于比较繁琐而易出现错误。

知识点

函数的单调性及单调区间导数的几何意义导数的运算

题型：简答题

简答题 · 13 分

18．已知函数，函数，其中．

（Ⅰ）如果函数与在处的切线均为，求切线的方程及的值；

（Ⅱ）如果曲线与有且仅有一个公共点，求的取值范围。

正确答案

（Ⅰ），；

（Ⅱ），或．

解析

试题分析：本题属于导数的应用的基本问题，题目的难度是逐渐由易到难，（1）直接按照步骤来求，（2）要注意作差构造新函数

（Ⅰ）解：求导，得，，．

由题意，得切线l的斜率，即，解得．

又切点坐标为，所以切线l的方程为．

（Ⅱ）解：设函数，．

“曲线与有且仅有一个公共点”等价于“函数有且仅有一

个零点”．

求导，得．

① 当时，

由，得，所以在单调递增．

又因为，所以有且仅有一个零点，符合题意．

②当时，

当变化时，与的变化情况如下表所示：

所以在上单调递减，在上单调递增，

所以当时，，

故有且仅有一个零点，符合题意．

③ 当时，

令，解得．

当变化时，与的变化情况如下表所示：

所以在上单调递减，在上单调递增，

所以当时，．

因为，，且在上单调递增，

所以．

又因为存在，，

所以存在使得，

所以函数存在两个零点，1，与题意不符．

综上，曲线与有且仅有一个公共点时，的范围是，或

考查方向

本题主要考查了导数的几何意义、利用导数研究函数的零点，导数作为一种工具，其应用主要分以下几类：

1．利用导数研究函数的单调性，

2．利用导数研究函数的极值、最值，

3．利用导数研究函数的零点个数，

4．利用导数研究不等式恒成立问题．

解题思路

本题考查导数的几何意义、导数在研究函数的应用，解题步骤如下：

1．求导，利用导数的几何意义得到等式，求出值和切线方程；

2．作差构造函数，将问题转化为函数有且只有一个零点；

3．求导，通过导函数的符号研究函数的单调性与极值；

4．通过研究极值的符号得到答案．

易错点

忽视新函数的定义域

知识点

函数零点的判断和求解导数的几何意义直线的一般式方程

题型：简答题

简答题 · 12 分

21．已知函数（为自然对数的底数，为常数）在点处的切线斜率为．

（Ⅰ）求的值及函数的极值；

（Ⅱ）证明：当时，；

（Ⅲ）证明：对任意给定的正数，总存在，使得当，恒有．

正确答案

（Ⅰ）见解析

（Ⅱ）见解析

（Ⅲ）见解析

解析

（Ⅰ）解,由，得．

因为,所以．

所以，．

令,得．

当时, 单调递减；当时, 单调递增．

所以当时, 取得极小值,且极小值为无极大值．

（Ⅱ）证明,令,则．

由（Ⅰ）得,故在R上单调递增．

所以当时，，即．

（Ⅲ）证明一,①若,则．

由（Ⅱ）知，当时，．所以当时, ．

取,当时，恒有．

②若,令,

要使不等式成立，只要成立．

而要使成立，则只要,只要成立．

令,则．

所以当时, 在内单调递增．

取,所以在内单调递增．

又，

易知．

所以．即存在,当时，恒有．

综上，对任意给定的正数，总存在,当时,恒有．

证明二,对任意给定的正数，取，

由（Ⅱ）知，当时，，所以．

当时，．

因此，对任意给定的正数，总存在,当时,恒有．

证明三,首先证明当时，恒有．

令，则．

由（Ⅱ）知，当时，，

从而，在上单调递减。

所以，即．

取，当时，有．

因此，对任意给定的正数，总存在,当时,恒有．

考查方向

本题考查导数与函数极值问题。

解题思路

易错点

第一问建议做出极值表便于观察，防止出错；

第二问忽略证明第一问时得到的结论。

知识点

导数的几何意义导数的运算不等式恒成立问题

继续学习学习下一知识点

下一知识点 : 导数的运算

百度题库 > 高考 > 理科数学 > 导数的几何意义

扫码查看完整答案与解析