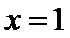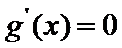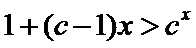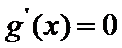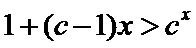- 导数的几何意义
- 共149题
设直线l1,l2分别是函数f(x)= 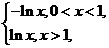
正确答案
知识点
15.已知f(x)为偶函数,当

正确答案
知识点
已知函数
24.设


25. 若对于任意


26.若



正确答案
解析



则



考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析
由题意得
令


此时

∵


因此实数

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
正确答案

解析


由




而


因此







则




① 若








因此









则
② 若



可得
由
因此
因此


因此

考查方向
解题思路
易错点
基本不等式的应用,分类讨论思想,函数与方程思想
已知函数
24.证明:当
25.证明:当

26.确定k的所以可能取值,使得存在


正确答案
(Ⅰ)详见解析
解析
解法一:(1)令
当



故当



考查方向
解题思路
求导,然后分类讨论求单调性
易错点
导数和函数的关系掌握不牢,不会利用导数判断函数的单调性
正确答案
(Ⅱ)详见解析
解析
(2)令

当



故对任意正实数
当


取






综上,当



考查方向
解题思路
先构造函数,然后求导判断单调区间,利用函数的单调性证明不等式。
易错点
不会构造函数,不会建立函数与导数之间的联系
正确答案
(Ⅲ) 
解析
(3)当



令
则有
故当





当



此时
令
则有
故当



故




则当
当

令
当




故当

综上,
考查方向
解题思路
分K大于1.K小于1和K等于1把不等式的左边去掉绝对值,然后再进行分类讨论,可得答案。
易错点
计算能力弱,求导分类讨论或重或漏
设函数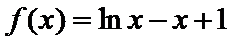
25.讨论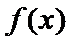
26.证明当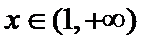
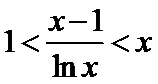
27.设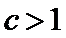
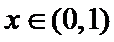
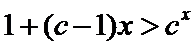
正确答案
(Ⅰ)当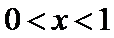
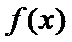
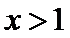
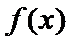
解析
(I)由题设,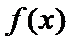
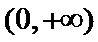
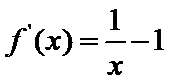
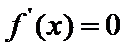
当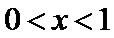
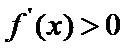
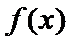
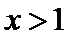
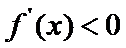
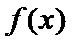
考查方向
解题思路
(I)首先求出导函数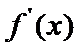
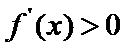
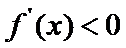
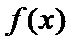
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅱ)(II)由(I)知,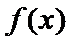
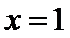
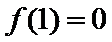
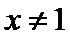
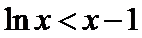
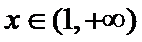
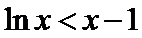
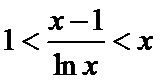
解析
(II)由(I)知,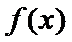
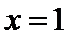
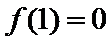
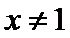
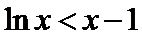
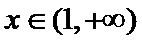
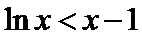
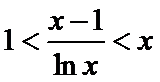
考查方向
解题思路
(II)左端等式可利用(I)的结论证明,右端将左端的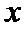

易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
正确答案
(Ⅲ)(III)由题设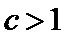
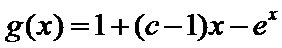
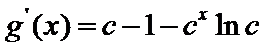
解得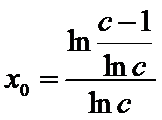
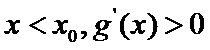
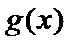
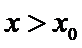
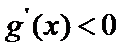
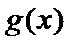
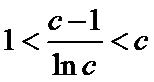
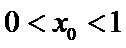
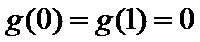
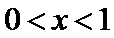
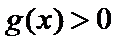
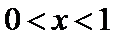
解析
(III)由题设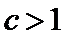
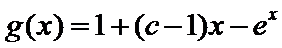
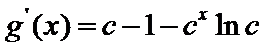
解得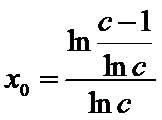
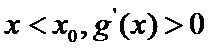
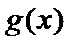
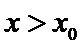
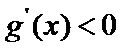
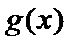
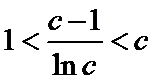
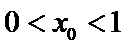
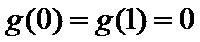
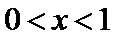
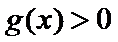
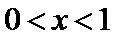
考查方向
解题思路
变形所证不等式构造新函数,然后通过利用导数研究函数的单调性来处理
易错点
对利用导数研究函数的单调性和不等式的证明与解法理解出现错误、计算错误
扫码查看完整答案与解析