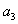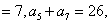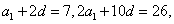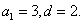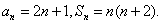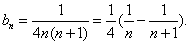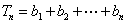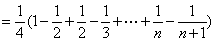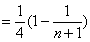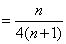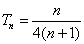- 等差数列的性质及应用
- 共275题
设数列{an},{bn}都是等差数列,若a1+b1=7,a3+b3=21,则a5+b5=__________.
正确答案
35
解析
∵{an},{bn}均是等差数列,根据等差数列的性质可得a1+a5=2a3,b1+b5=2b3,即a5=2a3-a1,b5=2b3-b1,
∴a5+b5=2(a3+b3)-(a1+b1)=2×21-7=35.
知识点
函数y=x2(x>0)的图像在点(ak,ak2)处的切线与x轴交点的横坐标为ak+1,k为正整数,a1=16,则a1+a3+a5=____▲_____
正确答案
21
解析
考查函数的切线方程、数列的通项。
在点(ak,ak2)处的切线方程为:


所以
知识点
已知等差数列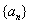
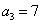
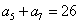
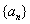
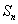
(1) 求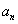
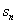
(2) 令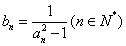
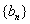
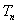
正确答案
见解析。
解析
(1)设等差数列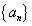
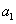
由于
所以
解得
由于
(2)因为 
因此
故
所以数列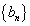
知识点
已知a是给定的实常数,
设函数

(1)求b的取值范围;
(2)设






正确答案
见解析
解析
(1)解:
令
则
于是可设

1)当


2)当


故
即
所以
所以

(2)解:由(Ⅰ)可知,假设存了

1)当
于是
即
此时
或
2)当
①若
于是
即
于是
此时
②若
于是
即
于是
此时
综上所述,存在
当
当
当
知识点
已知数列



(1)若



(2)证明:数列




正确答案
见解析
解析
(1)对任意

即

(2)①必要性:若数列




即




②充分性:若对于任意


则
于是
即
由



因为




综上所述,数列



知识点
扫码查看完整答案与解析