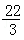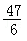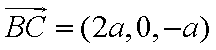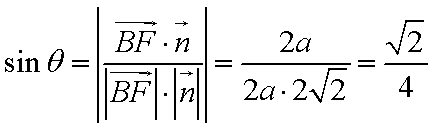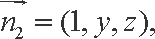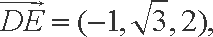- 空间图形的公理
- 共69题
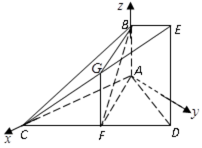
如图,在长方形








(1)在线段



(2)若面


正确答案
见解析。
解析
(1)
线段




证明如下:
设



又因为


所以









(2)











由此可以

因为








因为



又可得:


设面
由



所以


知识点
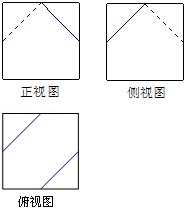
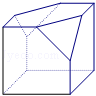
一个棱长为2的正方体沿其棱的中点截去部分后所得几何体的三视图如图示,则该几何体的体积为( )
正确答案
解析
依题意可知该几何体的直观图如图示,其体积为正方体的体积去掉两个三棱锥的体积,即: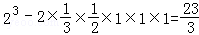
故选D。
知识点
如图,已知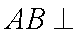
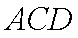
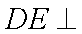
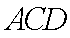
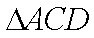
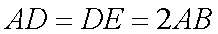
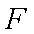
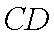
(1)求证: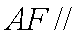
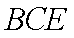
(2)求证:平面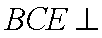
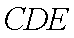
(3)求直线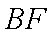
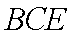
正确答案
见解析。
解析
(1) 证明:取
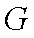
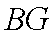
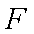
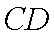
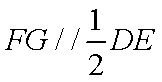
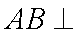
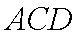
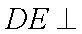
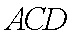
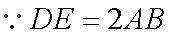
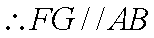
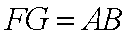
从而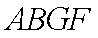
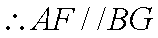
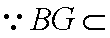
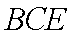
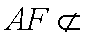
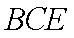
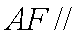
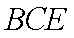
(2) 证明: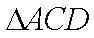
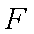
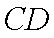
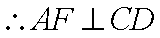
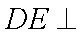
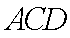
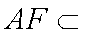
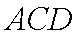
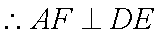
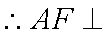
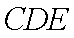
由 (1)知: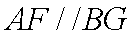
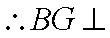
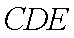
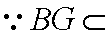
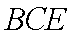

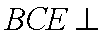
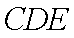
(3) 解:
设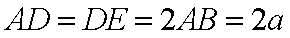
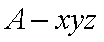
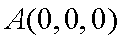
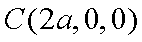
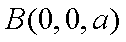
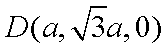
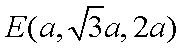
∵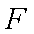
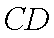
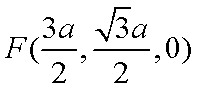
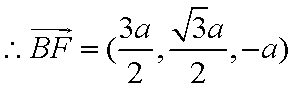
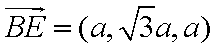
设平面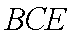
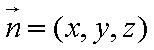
由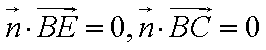
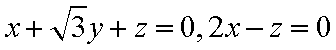
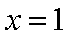
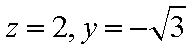
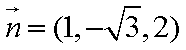
设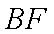
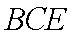
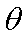
∴直线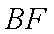
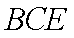
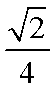
知识点
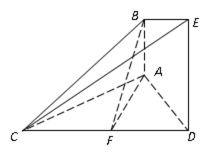
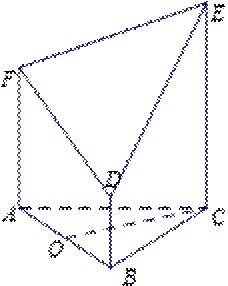
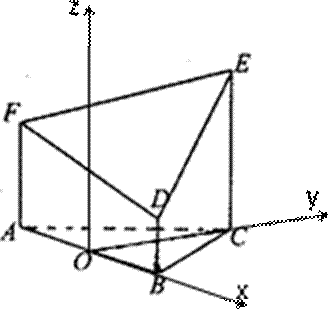
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,
正确答案
解析
(1)证法一: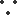
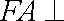
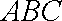

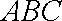

又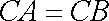

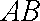
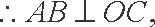


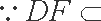


证法二:
如图,以


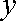
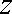
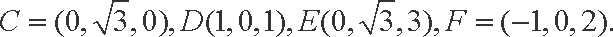
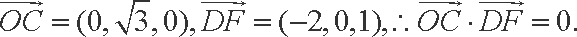

(2)解法一:
设平面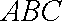
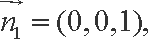
设平面
由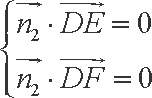
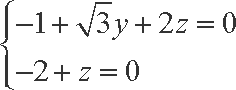
解得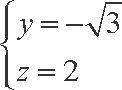
所以 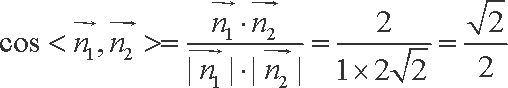
故平面
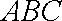

知识点
如图,某种水箱用的“浮球”,是由两个半球和一个圆柱筒组成. 已知球的直径是

(1)这种“浮球”的体积是多少
(2)要在这样

正确答案
(1)169.9

解析
解析:(1)





(2)

1个“浮球”的表面积
2500个“浮球”的表面积的和
所用胶的质量为
答:这种浮球的体积约为

知识点
扫码查看完整答案与解析