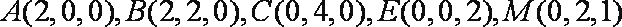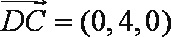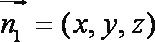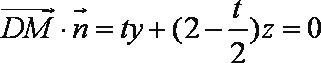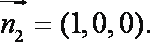空间图形的公理
共69题

· 空间图形的公理

空间图形的公理
共69题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

已知某四棱锥，底面是边长为2的正方形，且俯视图如右图所示.若该四棱锥的侧视图为直角三角形，则它的体积为__________。

正确答案

解析

易知

知识点

空间图形的公理

题型：单选题

单选题 · 5 分

设实数满足条件,若目标函数的最大值为12,则的最小值为（）

正确答案

解析

不等式表示的平面区域如图所示阴影部分,

当直线ax+by=z（a＞0,b＞0）
过直线4x-y-10=0与直线x-2y+8=0的交点（4,6）时,目标函数z=ax+by（a＞0,b＞0）取得最大12

∴4a+6b=12即2a+3b=6

则,当且仅当即时取等号,故选A.

知识点

空间图形的公理

题型：简答题

简答题 · 12 分

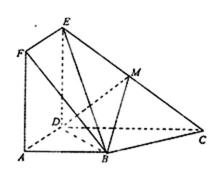
如图，正方形ADEF与梯形ABCD所在平面互相垂直，AD⊥CD，AB//CD，AB=AD=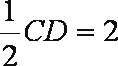，点M在线段EC上且不与E、C重合。

（1）当点M是EC中点时，求证：BM//平面ADEF；

（2）当平面BDM与平面ABF所成锐二面角的余弦值为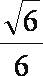时，求三棱锥M—BDE的体积.

正确答案

见解析

解析

（1）以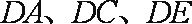分别为轴建立空间直角坐标系

则

的一个法向量

，。即 ………………………..4分

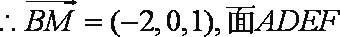
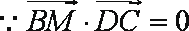
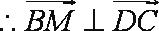
（2）依题意设，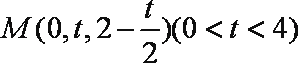

设面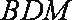的法向量

则，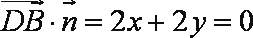

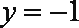
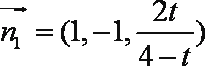
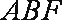
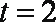
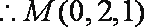
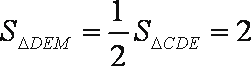
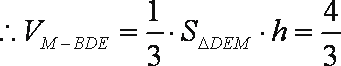
令，则，面的法向量

，解得………………10分

为EC的中点，，到面的距离

…………………………………………………………12分

另解：用传统方法证明相应给分。

知识点

空间图形的公理

题型：简答题

简答题 · 12 分

如图，在中，，斜边。可以通过以直线为轴旋转得到，且二面角是直二面角，动点的斜边上。

（1）求证：平面平面；

（2）当为的中点时，求异面直线与所成角的大小；

（3）求与平面所成角的最大值。

正确答案

见解析

解析

解析：（1）由题意，，，是二面角的平面角，

又二面角是直二面角，，又，

平面，又平面。平面平面。 --------4分

（2）作，垂足为，连结，则，

是异面直线与所成的角。 - -------------------------5分

在中，，，，又。在中，。 ----------7分

异面直线与所成角的大小为。 --------------------8分

（3）由（I）知，平面，是与平面所成的角，且，当最小时，最大………………10分

这时，，垂足为，，，

与平面所成角的最大值为。- ----------------------12

知识点

空间图形的公理

题型：简答题

简答题 · 10 分

如图，四棱锥中，底面ABCD是矩形，⊥平面ABCD，且，，点E是AB上一点，AE等于何值时，二面角的平面角为。

正确答案

见解析。

解析

以D为原点，射线DA、DC、DP为轴正方向建立空间直角坐标系，

设，则，

设平面的法向量为

，　　　　

记

而平面ECD的法向量，　　

则二面角D1—EC—D的平面角

。

当AE=时，二面角的平面角为。

知识点

空间图形的公理

继续学习学习下一知识点

下一知识点 : 异面直线及其所成的角

百度题库 > 高考 > 理科数学 > 空间图形的公理

扫码查看完整答案与解析