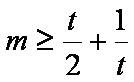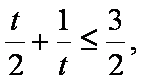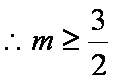- 空间图形的公理
- 共69题
已知函数
(1)求实常数
(2)设




正确答案
(1)
解析
(1)
所以,当

(2)由


设



所以,

知识点
如图,在直三棱柱








(1)求证:
(2)求二面角
正确答案
见解析。
解析
(1)连接

∵



面

∴



∴



∴

(2)∵在直三棱柱

∴
以



由(1)知

∴点




设平面

∵

∴


同理,平面

设二面角

则
∴
知识点
如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上。
(1)设AD=x(x
(2)如果DE是灌溉水管,为节约成本,希望它最短,DE的位置应在哪里?如果DE是参观线路,则希望它最长,DE的位置又应在哪里?请给予证明。
正确答案
见解析
解析
(1)在△ADE中,由余弦定理得:

又
把代入得
∴
∵ 
即函数的定义域为
(2)如果DE是水管,则
当且仅当


如果DE是参观线路,记
∴函数


故
∴
即DE为AB中线或AC中线时,DE最长.…………………………………………… 12分
知识点
已知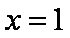
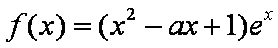
(1)求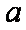
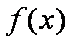
(2)若对于任意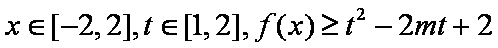
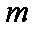
正确答案
见解析。
解析
(1)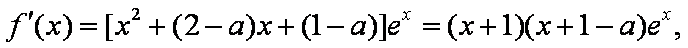
由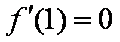
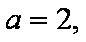
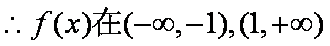
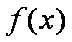
(2)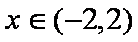
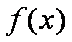
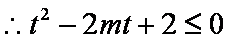
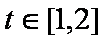
易知: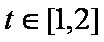
知识点
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°。
(1)求证:BD⊥平面PAC;
(2)若PA=AB,求PB与AC所成角的余弦值;
(3)当平面PBC与平面PDC垂直时,求PA的长。
正确答案
见解析
解析
(1)证明:因为四边形ABCD是菱形, 所以AC⊥BD。
又因为PA⊥平面ABCD, 所以PA⊥BD,
所以BD⊥平面PAC。
(2)设AC∩BD=O。 因为∠BAD=60°,PA=AB=2, 所以BO=1,AO=CO=
如图,以O为坐标原点,OB、OC所

P(0,-


所以=(1,

设PB与AC所成角为θ,则

(3)由(2)知=(-1,
设P(0,-

设平面PBC的法向量m=(x,y,z), 则·m=0,·m=0。
所以 



同理,可求得平面PDC的法向量n=
因为平面PBC⊥平面PDC, 所以m·n=0,即-6+

所以当平面PBC与平面PDC垂直时,PA=
知识点
扫码查看完整答案与解析