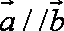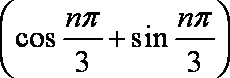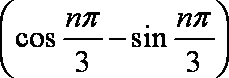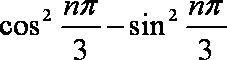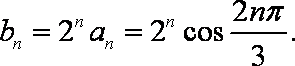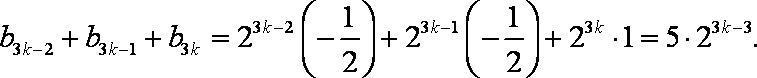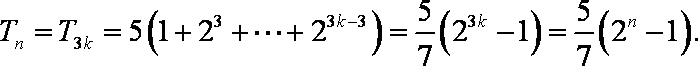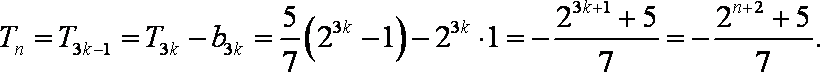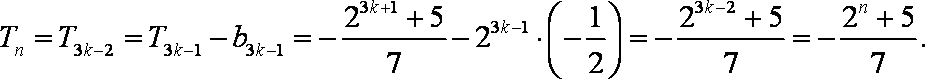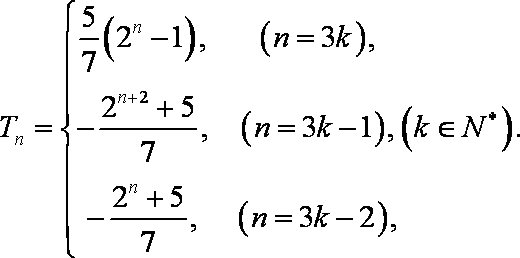- 等差数列的判断与证明
- 共95题
正数列




(1)求证:
(2)若数列
(3)若数列

正确答案
见解析
解析
(1)



(2)计算
根据数列是隔项成等差,写出数列的前几项:




当
所以




所以当

当
(3)因为数列
化简

设







只有
此时
或者
等差数列的前几项:



因为数列


此时
如果没有理由,猜想:


知识点
对大于或等于






根据上述分解规律,则


正确答案
9
解析
略
知识点
如下列所示,由若干个点组成形如三角形的图形,每条边(包括两个端点)有


正确答案

解析
略
知识点
对于任意的







(1)








(2)若各项为正数的等比数列







(3)若数列









正确答案
见解析
解析
解析:(1)在数列




在数列












(2)因为数列

将


解得

所以


对于任意的


所以数列数列


(3)由于

由于任意



即

即






即


只需

由① ②得

经检验

知识点
记数列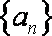
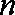
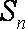
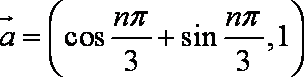
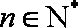
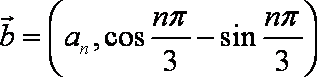
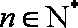
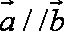
(1)求数列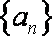
(2)求
(3)设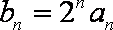
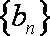
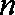
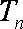
正确答案
见解析
解析
(1)∵
∴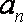
=
=
∴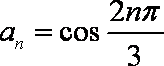
(2)数列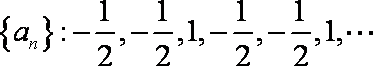
(3)
当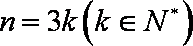
∵
∴
当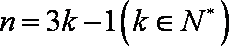
当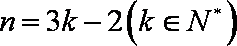
故
知识点
扫码查看完整答案与解析