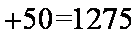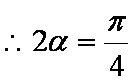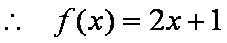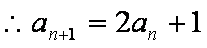- 等差数列的判断与证明
- 共95题
已知数列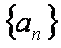
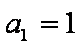

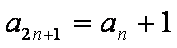
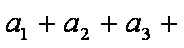
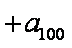
正确答案
1306
解析
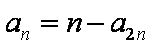
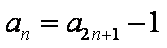

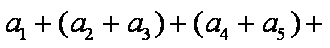
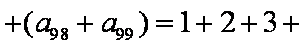
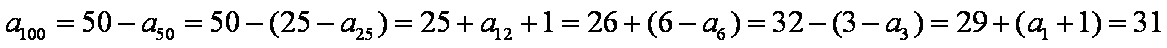

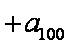
知识点
已知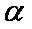
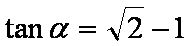
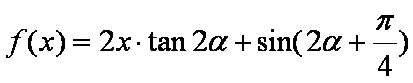
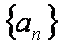
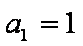
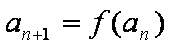
(1)求函数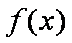
(2)求数列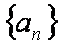
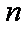
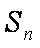
正确答案
(1)
解析
(1)由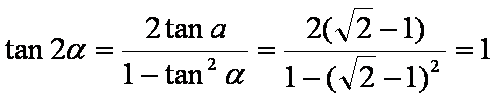
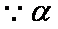
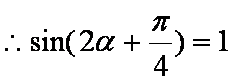
(2)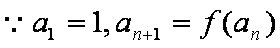
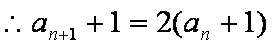

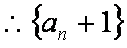
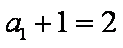
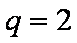
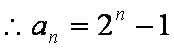
∴
知识点
设f1(x)=

(1) 求数列{an}的通项公式;
(2) 若

Qn的大小,并说明理由.
正确答案
见解析。
解析
(1)∵f1(0)=2,a1=


∴an+1=




∴数列{an}是首项为

(2)∵
∴





= a 2+2a 3+…+(2n-1)a2 n-na2 n.两式相减,得
当n=1时,

当n=2时,

当n≥3时,
知识点
已知数列




(1)证明:数列
(2)求数列


正确答案
见解析
解析
解析:
(1) ∵



∴设

由上可知,数列

(2)由(1)知,

∴
即
令
则
②-①,得
∴
知识点
已知数列



(1)求数列
(2)令



正确答案
(1)
解析
解析: (1)因为

又

(2) 易得

所以
所以 
知识点
扫码查看完整答案与解析