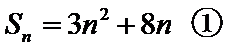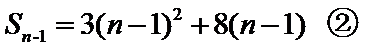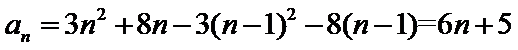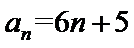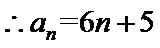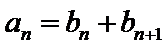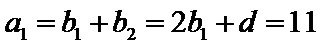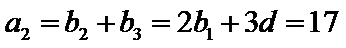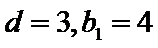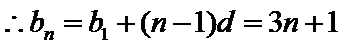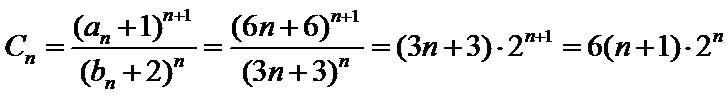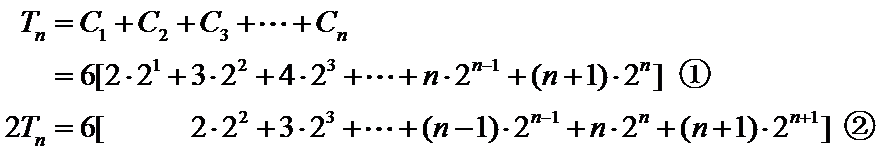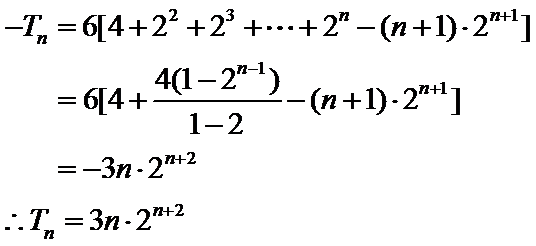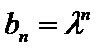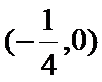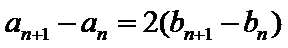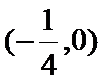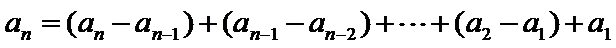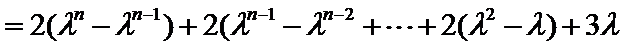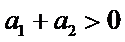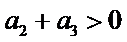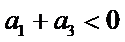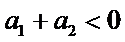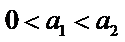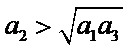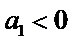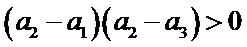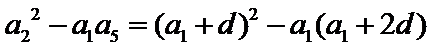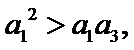- 等差数列的判断与证明
- 共95题
已知数列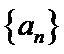
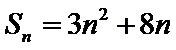
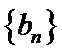
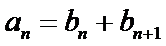
21.求数列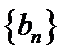
22.令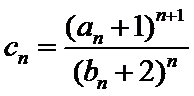
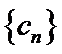
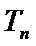
正确答案
(Ⅰ)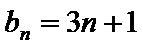
解析
(Ⅰ)
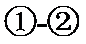
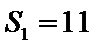
由
解得:
考查方向
解题思路
根据和与通项的关系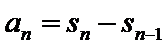
易错点
错位相减法:适合等差数列与等比数列的积数列的求和,写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
正确答案
(Ⅱ)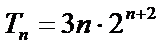
解析
(Ⅱ)
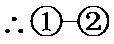
考查方向
解题思路
根据和与通项的关系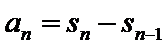
易错点
错位相减法:适合等差数列与等比数列的积数列的求和,写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
已知数列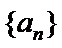
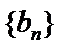
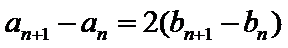
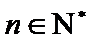
27. 若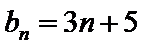
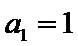
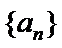
28. 设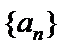
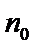
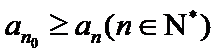
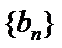
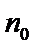
29. 设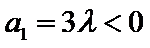
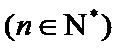
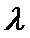
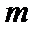
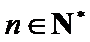
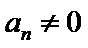
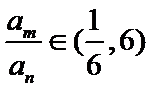
正确答案
(1)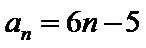
解析
试题分析: (1)把bn=3n+5代入已知递推式可得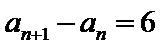
(1)因为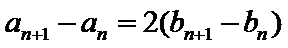
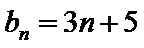
所以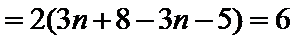
所以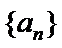
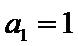
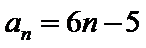
考查方向
解题思路
数列是高中数学的重要内容之一,是衔接初等数学与高等数学的桥梁,在高考中的地位举足轻重,近年来的新课标高考都把数列作为核心内容来加以考查,并且创意不断,常考常新.
易错点
等差数列性质的灵活运用
正确答案
(2)略
解析
试题分析:(2)由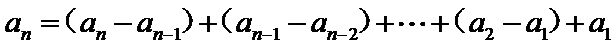
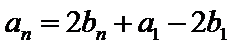
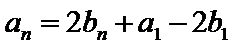
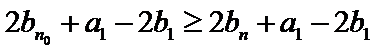
(2)由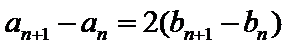
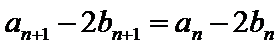
所以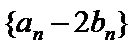
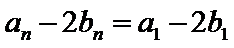
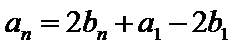
因为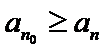
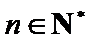
所以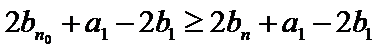
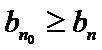
所以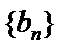
考查方向
解题思路
数列是高中数学的重要内容之一,是衔接初等数学与高等数学的桥梁,在高考中的地位举足轻重,近年来的新课标高考都把数列作为核心内容来加以考查,并且创意不断,常考常新.
易错点
数列的单调性
正确答案
(1)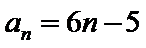
解析
试题分析:(3)由(2)可得an=2λn+λ,然后分-1<λ<0,λ=-1,λ<-1三种情况求得an的最大值M和最小值m,再由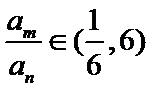
(3)因为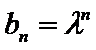
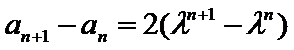
当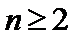
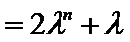
当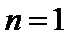
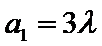
所以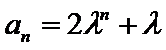
因为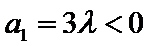
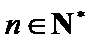
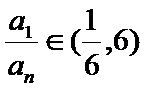
故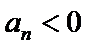
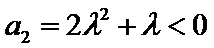
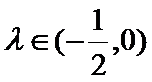
此时对任意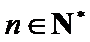
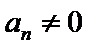
当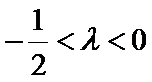
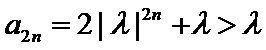
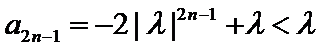
由指数函数的单调性知,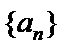
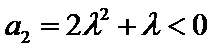
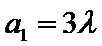
由题意,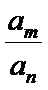
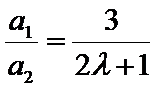
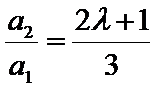
由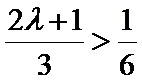
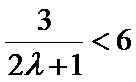
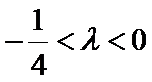
综上所述,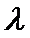
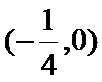
考查方向
解题思路
数列是高中数学的重要内容之一,是衔接初等数学与高等数学的桥梁,在高考中的地位举足轻重,近年来的新课标高考都把数列作为核心内容来加以考查,并且创意不断,常考常新.
易错点
分类讨论的不重不漏
6.设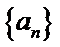
正确答案
解析
先分析四个答案支,A举一反例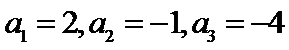
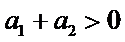
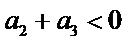
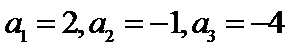
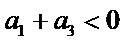
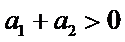
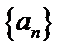
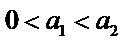
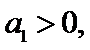
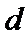
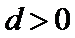
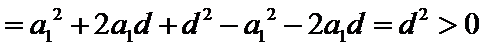
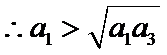
考查方向
解题思路
由于前两个选项无法使用公式直接做出判断,因此学生可以利用举反例的方法进行排除,这需要学生不能死套公式,要灵活应对,作差法是比较大小常规方法,对判断第三个选择只很有效.
易错点
等差数列性质的正确理解
知识点
已知各项都为正数的数列


17.求
18.求
正确答案
(Ⅰ)
解析
(Ⅰ)由题意得
考查方向
解题思路
(Ⅰ)将



易错点
对数列的递推公式;等
正确答案
(Ⅱ)
解析
(II)由
由于
故

考查方向
解题思路
(Ⅱ)将已知的递推公式


易错点
对数列的递推公式;等
20.(本小题满分12分)
已知数列

(Ⅰ)求数列
(Ⅱ)另

正确答案
(Ⅰ)

解析
(Ⅰ)


由
解得:
(Ⅱ)

考查方向
解题思路
根据和与通项的关系
易错点
错位相减法:适合等差数列与等比数列的积数列的求和,写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式.
知识点
扫码查看完整答案与解析