- 直角三角形的射影定理
- 共6题
1
题型:简答题
|
选修4-1:几何证明选讲
如图所示,AC为⊙O的直径,D为弧BC的中点,E为BC的中点.
28.求证:DE∥AB;
29.求证:ACBC= 2ADCD.
第(1)小题正确答案及相关解析
正确答案
详见解析
解析
(Ⅰ)连接

所以
因为


因为

所以
考查方向
圆切线的判定和证明
解题思路
作切线,然后找角的等量关系,然后证明平行
第(2)小题正确答案及相关解析
正确答案
详见解析
解析
(Ⅱ)因为

又





所以


考查方向
与圆有关的比例线段,相似三角形的性质和判定
解题思路
先证明三角形DAC和三角形ECD相似,然后得到比例式,进而转换成证明结论
1
题型:填空题
|
如图所示,AB是圆的直径,点C在圆上,过点B,C的切线交于点P,AP交圆于D,若AB=2,AC=1,则PC=______,PD=______,
正确答案

解析
略
知识点
直角三角形的射影定理
1
题型:
单选题
|
如图,







正确答案
B
解析
略
知识点
直角三角形的射影定理
1
题型:填空题
|
如图,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,AB=BC=3,
正确答案

解析
略
知识点
直角三角形的射影定理
1
题型:简答题
|
如图,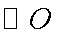
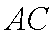
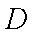
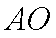
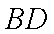
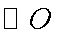
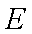
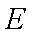
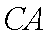
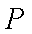
求证: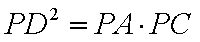
正确答案
见解析
解析
证明:连结OE,因为PE切⊙O于点E,所以∠OEP=900,所以∠OEB+∠BEP=900,因为OB=OE,所以∠OBE=∠OEB,因为OB⊥AC于点O,所以∠OBE+∠BDO=900
故∠BEP=∠BDO=∠PDE,PD=PE,又因为PE切⊙O于点E,所以PE2=PA·PC,
故PD2=PA·PC
知识点
直角三角形的射影定理
下一知识点 : 圆周角定理
扫码查看完整答案与解析