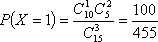- 系统抽样方法
- 共24题
某商场举办促销抽奖活动,奖券上印有数字100,80,60,0,凡顾客当天在该商场消费每超过1000元,即可随机从抽奖箱里摸取奖券一张,商场即赠送与奖券上所标数字等额的现金(单位:元),设奖券上的数字为ξ,ξ的分布列如下表所示,且ξ的数学期望Eξ=22。
(1)求
(2)若某顾客当天在商场消费2500元,求该顾客获得奖金数不少于160元的概率。
正确答案
(1)
(2)0.0375
解析
(1)依题意,
所以 
因为 
所以
由 

(2)依题意,该顾客在商场消费2500元,可以可以抽奖2次。
奖金数不少于160元的抽法只能是100元和100元; 100元和80元; 100元和60元;80元和80元四种情况。
设“该顾客获得奖金数不少于160元”为事件A,
则
答:该顾客获得奖金数不少于160元的概率为0.0375。 ……………………13分
知识点
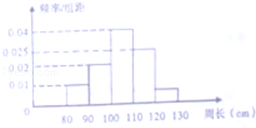
为了研究一片大约一万株树木的生长情况,随机测量了其中100株树木的底部周长(单位:cm),根据所得数据画出的样本频率分布直方图如图,那么在这片树木中底部周长大于100cm的株树大约中( )
正确答案
解析
由图可知:底部周长小于100cm段的频率为(0.01+0.02)×10=0.3,
则底部周长大于100cm的段的频率为1-0.3=0.7
那么在这片树木中底部周长大于100cm的株树大约10000×0.7=7000人。
故选C。
知识点
采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,……,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为
正确答案
解析
采用系统抽样方法从960人中抽取32人,将整体分成32组,每组30人,即





知识点
为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为

(3)根据表中数据估算两公司的每位员工在该月所得的劳务费。
正确答案
见解析
解析
(1)甲公司员工A投递快递件数的平均数为36,众数为33. ------------------------2分
(2)设
当




{说明:X取值都对给4分,若计算有错,在4分基础上错1个扣1分,4分扣完为止}

---------------------------------9分
{说明:每个概率值给1分,不化简不扣分,随机变量值计算错误的此处不再重复扣分}

(3)根据图中数据,可估算甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元. ---------------------------------13分
知识点
某工厂2011年生产的A,B,C,D四种型号的产品产量用条形图表示如图,现用分层抽样的方法从中选取50件样品参加今年五月份的一个展销会。
(1)问A,B,C,D型号的产品各抽取多少件?
(2)从50件样品中随机地抽取2件,求这2件产品恰好是不同型号产品的概率;
(3)50件样品中,从A,C型号的产品中随机抽取3件,用X表示抽取的A种型号产品的件数,求X的分布列和数学期望。
正确答案
见解析
解析
(1)从条形图上可知,共生产产品有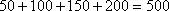
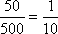
所以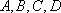
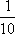
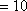
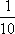
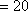
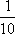
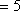
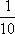
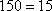
即样本中应抽取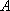

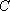
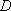
(2)从50件产品中任取2件共有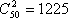
2件恰为同一产品的方法数为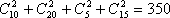
所以2件恰好为不同型号的产品的概率为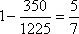
(3)解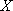

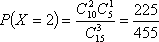

故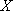
所以
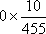
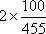
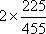
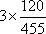
知识点
扫码查看完整答案与解析