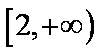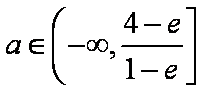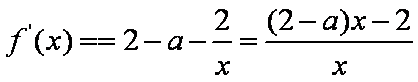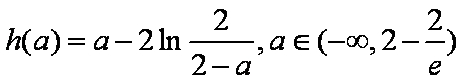- 指数函数单调性的应用
- 共75题
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
已知直线





正确答案
0或
解析
略
知识点
下列函数中,既是偶函数又在区间
正确答案
解析
略
知识点
正确答案
(1)
(2)在


解析
(1)由







又




(2)

则









①若


②若

③若


综上所述:
当



知识点
在二项式
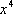
正确答案
10
解析
略
知识点
已知函数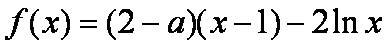
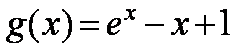
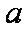
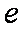
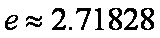
(1)当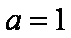
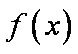
(2)若函数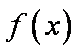
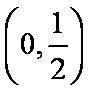
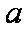
(3)若对任意给定的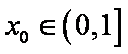
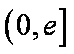
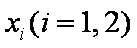
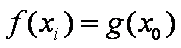
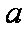
正确答案
(1)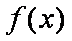
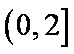
(2)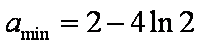
解析
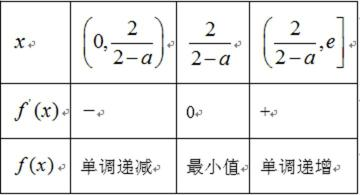
(1)当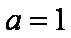
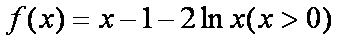
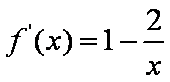
令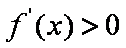
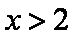
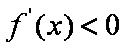
故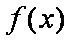
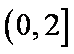
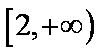
(2)∵函数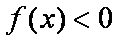
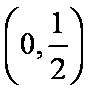
故要使函数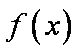
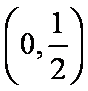
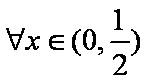
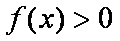
即对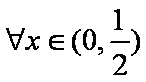

令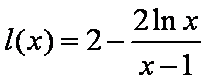
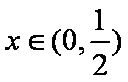
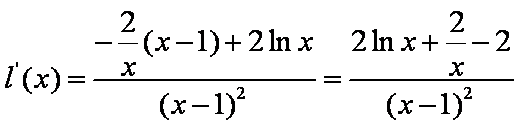
再令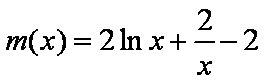
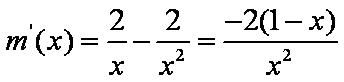
∵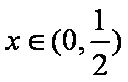
故函数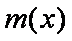
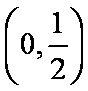
∴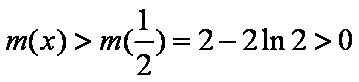
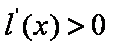
∴函数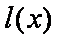

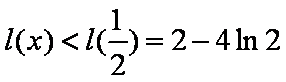
故只要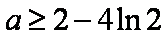
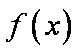
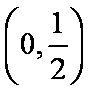
所以
(3)∵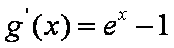
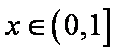
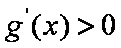
∴函数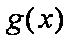
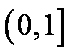
∴
当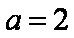
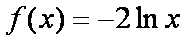
当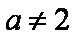
当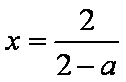
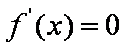
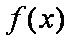
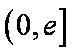
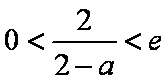
∴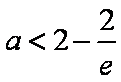
当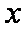
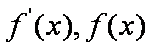
又因为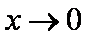
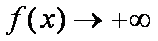
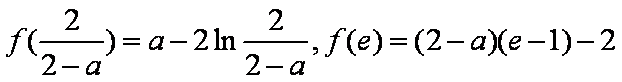
所以,对于给定的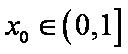
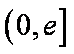
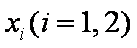
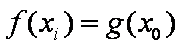
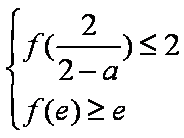
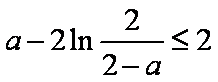
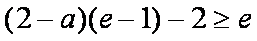
令
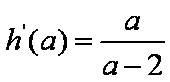
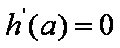
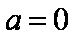
故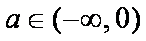
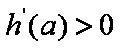
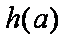
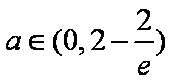
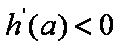
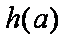
所以对任意的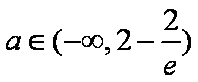
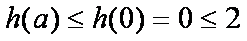
由③得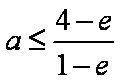
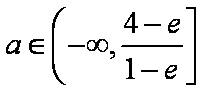
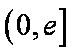
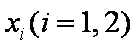
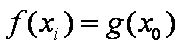
知识点
1.若集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设m为实数,函数

(1)若
(2)当m>0时,求证

(3)若


正确答案
(1)
当

当

解得

(2)由于
所以
任取

所以
即:

解二:由(2)结论得:

所以只要
得
当
当

综上得:
解析
解析已在路上飞奔,马上就到!
知识点
9.设集合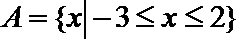
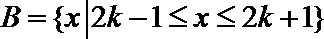
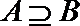
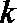
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析