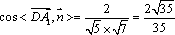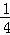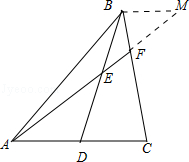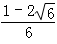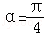- 直线方程和两条直线的位置关系
- 共650题
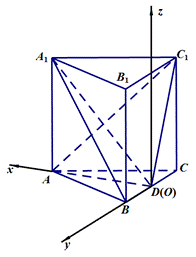
如图,直三棱柱ABC—A1B1C1中,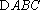
(1)求证:A1B//平面ADC1;
(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值。
正确答案
见解析
解析
(1)因为三棱柱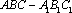
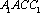
连结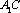
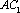
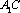
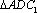
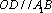
因为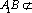
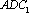
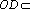
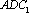
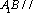
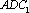
(2)因为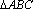
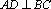
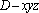
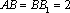
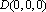
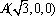
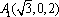
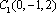
则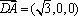
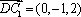
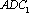
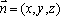
由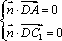
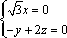
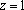
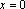
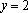
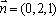
又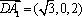
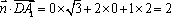
所以
设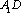
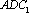

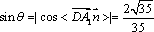
所以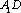
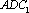
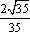
知识点
直线

正确答案
解析
略
知识点
如图,△













(1)求该几何体中间一个空心球的表面积的大小;
(2)求图中阴影部分绕直线
正确答案
(1)
解析
(1)连接

设

在

所以
所以
(2)





知识点
如图,直线










正确答案
解析
略
知识点
在△ BC中,D是边AC的中点,点E在线段BD上,且满足BE=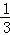
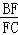
正确答案
解析
如图所示,
过点B作BM∥AC交BF的延长线于点M。
则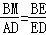
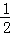
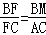
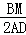
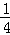
故答案为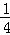
知识点
直线
正确答案
解析
略
知识点
在△


正确答案
解析
略
知识点
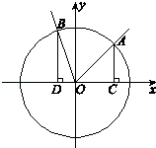
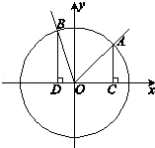
如图,在直角坐标系xOy中,角α的顶点是原点,始边与x轴正半轴重合,终边交单位圆于点A,且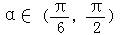
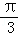
(1)若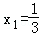
(2)分别过A,B作x轴的垂线,垂足依次为C,D,记△AOC的面积为S1,△BOD的面积为S2,若S1=2S2,求角α的值。
正确答案
(1)
(2)
解析
(1)解:由三角函数定义,得 x1=cosα,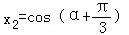
因为 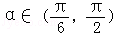
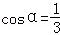
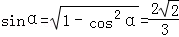
所以 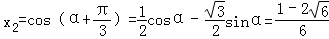
(2)解:依题意得 y1=sinα,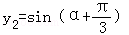
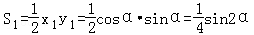

依题意S1=2S2 得 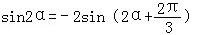


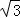
整理得 cos2α=0。
因为 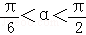
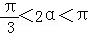
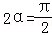
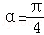
知识点
若圆





正确答案

解析
略
知识点
如图甲,设正方形











(1)证明:

(2)求平面

正确答案
见解析。
解析
(1)证明:在图甲中,易知

因为




(2)解法1、
如图,在图乙中作


由于


所以


所以


图甲中有


设




又由

于是,
在

解法2、
如图,在图乙中作











设





又由

于是,
在
作











显然,

设





设平面







知识点
扫码查看完整答案与解析