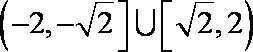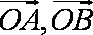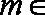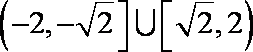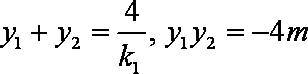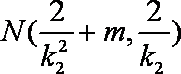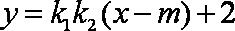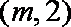- 直线方程和两条直线的位置关系
- 共650题
15.己知直线x+ y+m=0与圆x2+ y2 =2交于不同的两点A、B,O是坐标原点,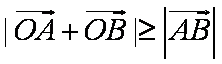
正确答案
解析
因为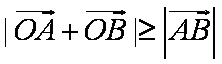
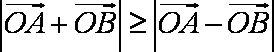


夹角


知识点
15.在平行四边形









正确答案
1
解析
略
知识点






正确答案
解析
连接BD、OD,如下图所示:
由已知中AB为圆O的直径,则∠ADB=90°
又∵CD为圆的切线,则CD2=CB•CA,即(2)2=CA,∴CA=4,∴AB=3,得圆的半径r=
在直角△CDO中,则sin∠DCA
知识点
已知动圆过定点P(2,0),且在y轴上截得弦长为4。
(1)求动圆圆心的轨迹Q的方程;
(2)已知点E(m,0)为一个定点,过E作斜率分别为k1、k2的两条直线交轨迹Q于点A、B、C、D四点,且M、N分别是线段AB、CD的中点,若k1 + k2 = 1,求证:直线MN过定点。
正确答案
见解析。
解析
(1)设动圆圆心为O1(x,y),动圆与y轴交于R,S两点,由题意,得|O1P|=|O1S|,
当O1不在y轴上时,过O1作O1H⊥RS交RS于H,则H是RS的中点,
∴|O1S|=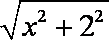
又|O1P|=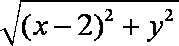
∴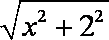
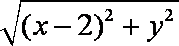
化简得y2=4x(x≠0)。
又当O1在y轴上时,O1与O重合,点O1的坐标为(0,0)也满足方程y2=4x,
∴动圆圆心的轨迹Q的方程为y2=4x
(2)由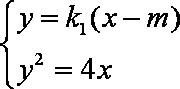
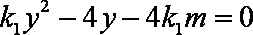
AB中点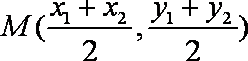
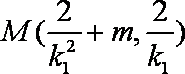
∴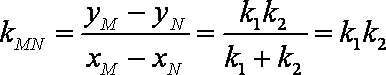
∴MN: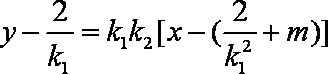
∴直线MN恒过定点
知识点
选修4-4:坐标系与参数方程
在直角坐标系






(1)求C1的直角坐标方程;
(2)当C1与C2有两个公共点时,求实数
正确答案
见解析。
解析
(1)曲线

∴曲线

(2)曲线

如下图所示,曲线

当直线



舍去

当直线



∴由图可知,当
曲线

知识点
选修4-4:坐标系与参数方程
以直角坐标系的原点











(1)求直线

(2)试判定直线

正确答案
见解析。
解析
本小题主要考查圆的参数方程、直线与圆的位置关系等基础知识,考查运算求解能力,满分7分。
(1)直线

圆C的极坐标方程为
(2)因为




所以直线
知识点
10.与圆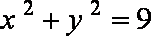
正确答案
解析
设所求圆的圆心C坐标为(x,y),则圆的半径为|x|,又与圆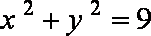
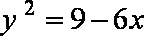
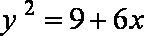

知识点
选修4—4:坐标系与参数方程
在直角坐标系


(1)求圆C的极坐标方程;
(2)直线



正确答案
见解析。
解析
(1)圆C的普通方程为
所以圆C的极坐标方程为
(2)设


设


所以
知识点
15.已知直线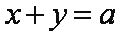
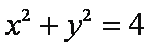
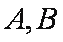

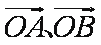
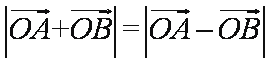
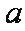
正确答案
±2
解析
因为向量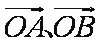
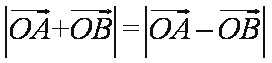
知识点
12.顶点在原点,经过圆

正确答案
解析
因为圆的圆心坐标为


知识点
扫码查看完整答案与解析