- 直线方程和两条直线的位置关系
- 共650题
11.直线x-2y+2=0过椭圆
正确答案

解析
直线x-2y+2=0与x轴的交点为(-2,0),即为椭圆的左焦点,故c=2.
直线x-2y+2=0与y轴的交点为(0,1),即为椭圆的顶点,故b=1.
故a2=b2+c2=5,椭圆方程为
知识点
选做题:第14.15题为选做题,考生只选做其中一题.
14.直线l的参数方程是

15.如图,⊙




交⊙



的大小为()
正确答案
14.
解析
略。
知识点
20.设函数F(x)在区间D上的导函数为F1(x),F1(x)在区间D上的导函数为F2(x),如果当x∈D时,F2(x)≥0,则称F(x)在区间D上是下凸函数.已知e是自然对数的底数,f(x)=ex-ax3+3x-6.
(1)若f(x)在[0,+∞)上是下凸函数,求a的取值范围;
(2)设M(x)=f(x)+f(-x)+12,n是正整数,求证:M(1)M(2)…M(n)>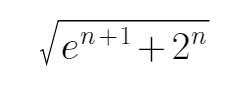
正确答案
见解析。
解析
(1)f′(x)=ex-3ax2+3,设F1(x)=f′(x),则F1′(x)=ex-6ax.
∵f(x)在[0,+∞)上是下凸函数,
∴当x∈[0,+∞)时,F1′(x)=ex-6ax≥0.
当x=0时,1≥0成立,即F1′(x)=ex-6ax≥0成立,此时a∈R.
当x∈(0,+∞)时,由F1′(x)=ex-6ax≥0得,
设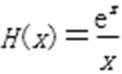
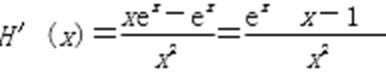
∴当x∈(1,+∞)时,H′(x)>0,H(x)单调递增;
当x∈(0,1)时,H′(x)<0,H(x)单调递减,
∴当x=1时,H(x)取得最小值H(1)=e,
∴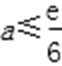
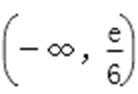
(2)∵f(x)=ex-ax3+3x-6,
∴M(x)=f(x)+f(-x)+12=ex+e-x>0.
∵M(x1)M(x2)=ex1+x2+ex1-x2+ex2-x1+e-x1-x2>ex1+x2+ex1-x2+ex2-x1,
又ex1-x2+ex2-x1≥
∴M(1)M(n)>en+1+2,M(2)M(n-1)>en+1+2,
M(3)M(n-2)>en+1+2,…,M(n)M(1)>en+1+2,
∴[M(1)M(n)][M(2)M(n-1)]· …·[M(n)M(1)]>(en+1+2)n,
∴M(1)M(2)· …·
知识点
16.在极坐标系中,点P(2,﹣

正确答案
3
解析
略。
知识点
正确答案
解析
略
知识点
19.已知函数

(1)当

(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若三条直线l1:x-y=0;l2:x+y-2=0; l3:5x-ky-15=0围成一个三角形,则k的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.从北京到西安的某三列火车正点到达的概率分别为
(1)这三列火车恰有两列正点到达的概率;
(2)这三列火车正点到达列数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.
正确答案
π2―2
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析






















