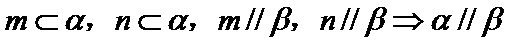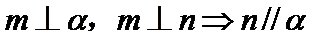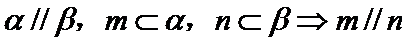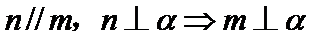- 直线方程和两条直线的位置关系
- 共650题
10.直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知直线





(1)求E的方程
(2)过圆
正确答案
(1)设椭圆半焦距为c,
圆心O到l的距离d=

∴直线l被圆O截得的弦长为

由2b=
解得b=
∵椭圆E:


∴
∴
∴椭圆E的方程为
(2)证明:设P(x0,y0),
过点P的椭圆E的切线l0的方程为y﹣y0=k(x﹣x0)
与椭圆方程联立,
消去y可得
(3+2k2)x2+4k(y0﹣kx0)x+2(kx0﹣y0)2﹣6=0
∴ △=[4k(y0﹣kx0)]2﹣4(3+2k2)[2(kx0﹣y0)2﹣6]=0
∴(

设满足题意的椭圆的两条切线的斜率分别为k1,k2,
∴ k1k2=﹣
∵ P在圆O上,∴
∴ k1k2=﹣
∴两切线斜率之积为定值﹣1.
解析
解析已在路上飞奔,马上就到!
知识点
9.直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知两条直线

正确答案
-3或1
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设a,b为两条直线,α、β为两个平面,下列四个命题中真命题是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知抛物线





(1)求证:直线
(2)分别以


正确答案
(1)证明:由题可知





所以,




同理可得:

直线


显然,不论


(2)过









即
又因为公共弦必与两圆的连心线垂直,所以公共弦的斜率为
所以,公共弦所在直线的方程为
即
所以公共弦恒过原点。
根据平面几何的知识知道:公共弦中点就是公共弦与两圆连心线的交点,所以原点




又对于圆上任意一点


解析
解析已在路上飞奔,马上就到!
知识点
6.已知直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知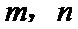
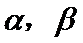
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.点(-2,1)到直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析