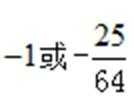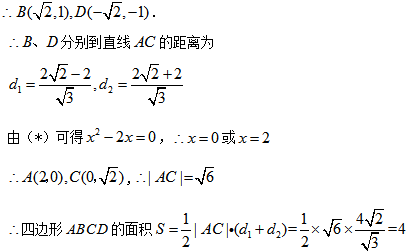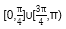- 直线方程和两条直线的位置关系
- 共650题
4.已知直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若存在过点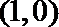
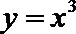
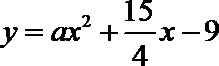
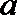
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知曲线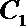
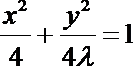
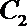
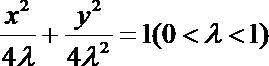
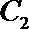
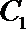
(1) 求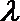
(2) 若曲线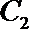
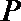
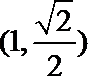
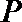
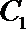
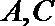
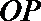
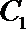
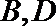
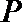
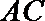
① 求直线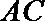
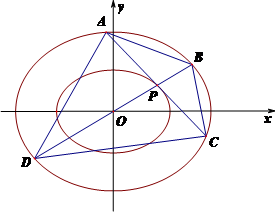
② 求四边形
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知直线l的倾斜角为α,且
正确答案
解析
当α从0°无限接近90°时,
斜率取值范围为[0,+∞);
当从90°无限接近135°时,
斜率取值范围为(-∞,-1].
知识点
6.已知圆P:x2+y2=4y及抛物线S:x2=8y,过圆心P作直线 l,此直线与上述两条曲线的四个交点,自左向右顺次记为A,B,C,D,如果|AB|,|BC|,|CD|按此顺序构成一个等差数列,则直线l的斜率为( ).
正确答案
解析
由题意可知,圆P的圆心坐标为(0,2),半径为2,抛物线S的焦点为(0,2),准线方程为y=-2,画出图象如图所示,其中|BC|=4.由于|AB|,|BC|,|CD|成等差数列,所以|AB|+|CD|=8,所以|AB|+|BC|+|CD|=12,则所求问题等价于当过抛物线S的焦点的直线被抛物线所截得的线段的长度为12时,求直线的斜率.设A(x1,y1),D(x2,y2),过A,D分别向抛物线的准线作垂线,垂足分别为A',D'.根据抛物线定义得|AP|=|AA'|=y1+2,|DP|=|DD'|=y2+2,所以|AD|=|AP|+|DP|=y1+y2+4=12,得y1+y2=8.由题意可知,直线l的斜率存在,且不为0.设直线l的斜率为k(k≠0),则直线l的方程为y=kx+2,即x=

知识点
6.下列四个函数图象,只有一个是符合y=|k1x+b1|+|k2x+b2|-|k3x+b3|(其中k1,k2,k3为正实数,b1,b2,b3为非零实数)的图象,则根据你所判断的图象,k1,k2,k3之间一定成立的关系是( ).
正确答案
解析
当x足够小时,y=-(k1+k2-k3)x-(b1+b2-b3),
当x足够大时,y=(k1+k2-k3)x+(b1+b2-b3),
可见折线的两端的斜率必定为相反数,
此时只有③符合条件.此时k1+k2-k3=0.
知识点
5.过点M(-2,0)的直线l与椭圆x2+2y2=2交于P1,P2,线段P1P2的中点为P。设直线l的斜率为k1(k1≠0),直线OP(O为坐标原点)的斜率为k2,则k1k2等于( )
正确答案
解析
设P1(x1,y1),P2(x2,y2),P(x0,y0),则






知识点
7.经过点P(0,-1)作直线l,若直线l与连接A(1,-2),B(2,1)的线段总有公共点,则直线l的斜率k和倾斜角α的取值范围分别为_________和_________。
正确答案
[-1,1]
解析
如图所示,结合图形,为使直线l与线段AB总有公共点,则kPA≤k≤kPB,而kPB>0,kPA<0,故当k<0时,倾斜角α为钝角,当k=0时,α=0,当k>0时,α为锐角。
又kPA=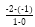
kPB=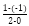
∴-1≤k≤1,即直线l的斜率k的取值范围为[-1,1].
又当0≤k≤1时,0≤α≤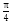
当-1≤k<0时,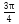
∴直线l的倾斜角α的取值范围为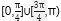
知识点
9.过点(

正确答案
-
解析
如图,



当∠AOB=
此时点O到AB的距离d=
设AB的方程为y=k(x-

由d=


知识点
扫码查看完整答案与解析