- 直线方程和两条直线的位置关系
- 共650题
17.已知抛物线






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知两条直线
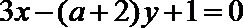
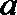
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知圆的方程x2+y2=4,若抛物线过点A(0,-1),B(0,1)且以圆的切线为准线,则抛物线的焦点轨迹方程是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆



( 1)求椭圆
(2)设点









正确答案
(1)依题意,设椭圆C的方程为=1(a>b>0),焦距为2c,
由题设条件知,a2=8,b=c, 所以b2=
故椭圆C的方程为
(2)椭圆C的左准线方程为x=-4,所以点P的坐标为(-4,0),
显然直线l的斜率k存在,所以直线的方程为y=k(x+4)。
如图,设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的
中点为G(x0,y0),
由
得(1+2k2)x2+16k2x+32k2-8=0 ①
由=(16k2)2-4(1+2k2)(32k2-8)>0
解得

因为x1,x2是方程①的两根,所以x1+x2=-
于是x0=

∵x0=
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
所以点G在正方形Q内(包括边界)的充要条件为

解得

故直线l斜率的取值范围是[

解析
解析已在路上飞奔,马上就到!
知识点
17.已知曲线 




(1)求
(2)若直线 



正确答案
(1)由

由



当

当

又∵点
∴切点
(2)∵直线

∴直线

∵


∴直线
即
解析
解析已在路上飞奔,马上就到!
知识点
1. 若函数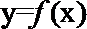
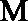
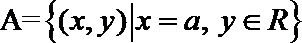
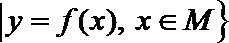

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 对于定义在上的函数
①若


②若对



③若函数


④函数


其中正确命题为 ( ) .
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{an}满足条件:a1=1,a2=r(r>0),且{anan+1}是公比为q(q>0)的等比数列,设bn=a2n-1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N*)成立的q的取值范围;
(2)求bn和
(3)设r=219.2-1,q=

正确答案
(1)
(2)
(3)最大项2.25 ,最小项-4
解析
解析已在路上飞奔,马上就到!
知识点
6. 







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析