- 直线方程和两条直线的位置关系
- 共650题
在直角坐标系




极坐标系(与直角坐标系
为极轴)中,直线


与




正确答案
解析
略
知识点
设

(1)求函数
(2)证明:
(3)设





令

(参考数据:



正确答案
见解析
解析
(1)因为f′(x)=(r+1)(1+x)r-(r+1)=(r+1)[(1+x)r-1],令f′(x)=0,解得x=0.
当-1<x<0时,f′(x)<0,所以f(x)在(-1,0)内是减函数;
当x>0时,f′(x)>0,所以f(x)在(0,+∞)内是增函数。
故函数f(x)在x=0处取得最小值f(0)=0.
(2)证明:由(1),当x∈(-1,+∞)时,有f(x)≥f(0)=0,即
(1+x)r+1≥1+(r+1)x,且等号当且仅当x=0时成立,
故当x>-1且x≠0时,有
(1+x)r+1>1+(r+1)x.①
在①中,令

上式两边同乘nr+1,得(n+1)r+1>nr+1+nr(r+1),即

当n>1时,在①中令

且当n=1时,③也成立。
综合②,③得

(3)解:在④中,令



……

将以上各式相加,并整理得

代入数据计算,可得

由[S]的定义,得[S]=211
知识点
某商场举行的“三色球”购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
其余情况无奖且每次摸奖最多只能获得一个奖级。
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额X的分布列与期望E(X)。
正确答案
见解析
解析
设Ai表示摸到i个红球,Bj表示摸到j个蓝球,
则Ai(i=0,1,2,3)与Bj(j=0,1)独立。
(1)恰好摸到1个红球的概率为
P(A1)=
(2)X的所有可能值为0,10,50,200,且
P(X=200)=P(A3B1)=P(A3)P(B1)=
P(X=50)=P(A3B0)=P(A3)P(B0)=
P(X=10)=P(A2B1)=P(A2)P(B1)=
P(X=0)=
综上知X的分布列为
从而有E(X)=0×



知识点
已知



正确答案
解析


另:
得:
知识点
设△ABC的内角A,B,C所对边的长分别为a,b,c.若b+c=2a,3sin A=5sin B,则角C=__________.
正确答案
解析
∵3sin A=5sin B,∴3a=5b.①
又∵b+c=2a,②
∴由①②可得,

∴

知识点
已知函数f(x)=4cos ωx·
(1)求ω的值;
(2)讨论f(x)在区间
正确答案
见解析
解析
解析:(1)f(x)=4cos ωx·sin
=

=

因为f(x)的最小正周期为π,且ω>0,
从而有
(2)由(1)知,f(x)=
若0≤x≤

当

当

综上可知,f(x)在区间

知识点
若

正确答案
4
解析
因为


知识点
如图,








正确答案
见解析
解析
要证









知识点
在等腰直角三角形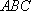
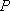
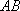
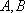
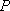
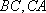
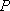
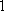
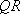
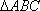
正确答案
解析
略
知识点
设i是虚数单位,

正确答案
解析
设z=a+bi(a,b∈R),则由
即(a2+b2)i+2=2a+2bi,
所以2a=2,a2+b2=2b,
所以a=1,b=1,即z=a+bi=1+i.
知识点
扫码查看完整答案与解析