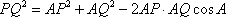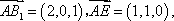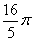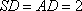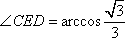- 直线方程和两条直线的位置关系
- 共650题
如图所示:圆

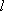
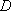
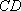
正确答案
解析
略
知识点
函数



正确答案
4
解析
略
知识点
如图5,AB是圆柱ABFG的母线,C是点A关于点B对称的点,O是圆柱上底面的圆心,BF过O点,DE是过O点的动直径,且AB=2,BF=2AB.
(1)求证:BE⊥平面ACD;
(2)当三棱锥D—BCE的体积最大时,求二面角C—DE—A的平面角的余弦值.
正确答案
见解析。
解析
(1)
证明:




∴


∵

∵
∵



∴BE⊥平面
(2)解:

设



当且仅当


∵三棱锥



∴三角形
此时,

∴
∵

连结CO,AO,
从而有


在三角形
又

同理可得



知识点
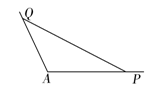
如图,角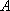
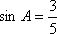
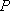
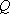
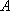
两边上不同于点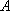
(1)若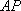
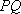
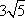
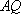
(2)设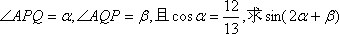
正确答案
见解析
解析
解:(1)
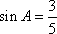
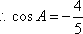
在
所以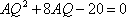
解得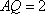
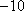
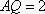
(2)由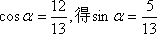
在三角形APQ中,
又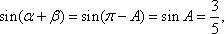
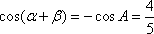
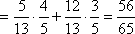
知识点
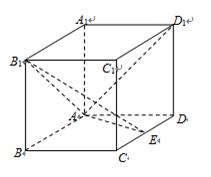
如图,在长方体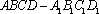
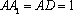
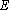
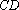
(1)求证: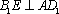
(2)若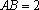
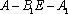
正确答案
见解析
解析
解析:(1)方法一、以A为坐标原点,以AB、AD、AA1分别为x轴、y轴、z轴方向建立空间直角坐标系,设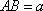
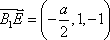
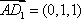
所以 , 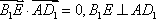
另解: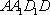
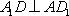
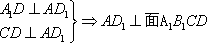
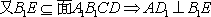
(2)因为
所以取面AB1E的一个法向量为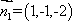
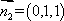
设二面角A-B1E-A1为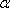
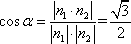
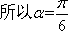
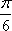
知识点
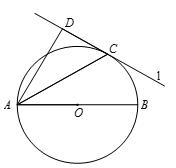
如图,A,B是圆O上的两点,且OA⊥OB,OA=2,C为OA的中点,连接BC并延长交圆O于点D,则CD= 。
正确答案
解析
略
知识点
已知直线







正确答案
解析
略
知识点
已知直线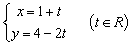
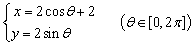
正确答案
解析
略
知识点
如图2,点





正确答案
2
解析
由已知





知识点
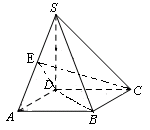
如图,四棱锥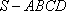
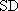
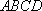
(1)求证: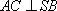
(2)求二面角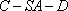
正确答案
见解析
解析
解析:(1)连接BD,∵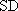
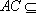
又四边形ABCD是正方形,∴AC⊥BD
∴AC ⊥平面SBD
∴AC⊥SB. ………………6分
(2)设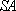
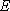
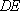
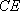
∵SD=AD,CS=CA,
∴DE⊥SA, CE⊥SA.
∴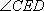
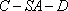
计算得:DE=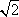
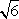
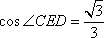
所以所求二面角的大小为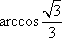
知识点
扫码查看完整答案与解析