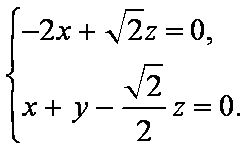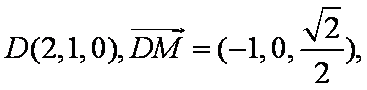- 直线方程和两条直线的位置关系
- 共650题
已知点A(1,-1),B(3,0),C(2,1),若平面区域D由所有满足=λ+μ(1≤λ≤2,0≤μ≤1)的点P组成,则D的面积为 。
正确答案
3
解析
如图:延长AB到D使BD=AB,作BF平行且等于AC,则点P组成的图形是以BD.BF为邻边的平行四边形,又BD=AB=


所以

知识点
在斜三棱柱





(1)求证:
(2)在侧棱



正确答案
见解析
解析
解析:(1)证:


又



(2)如图所示以点




建立空间直角坐标系




所以

由条件易得面

设平面

由
令

则
所以,当


知识点
如图,点A在直径为15的⊙O 上,PBC是过点O的割线,且PA=10,PB=5.。
(1)求证:PA与⊙O相切;
(2)
正确答案
见解析
解析
(1)证明:连结OA,因为⊙O的直径为15,所以OA=OB=7.5
又PA=10,PB=5,所以PO=12.5
在△APO中,PO2=156.25,PA2+OA2=156.25
即PO2= PA2+OA2,所以PA⊥OA,又点A在⊙O上
故PA与⊙O相切
(2)解:∵PA为⊙O的切线,∴∠ACB=∠PAB,
又由∠P=∠P, ∴△PAB∽△PCA,∴
设AB=k,AC=2k, ∵BC为⊙O的直径且BC=15 ,AB⊥AC
∴
∴
知识点
在极坐标



(1)求圆C的标准方程和直线
(2)若直线

正确答案
见解析
解析
(1)由
所以直线

由
又
所以,圆

(2)因为直线


两边平方得
所以a的取值范围是
知识点
如图所示,已知直四棱柱

(1)求证:
(2)求二面角
正确答案
解析
(1)设E是DC的中点,连接BE,
则四边形DABE为正方形,∴BE⊥CD,故BD=

∴∠DBC=90°,即BD⊥BC。
又BD⊥BB1,B1B∩BC=B
∴BD⊥平面BCC1B1。
(2)由(1)知DB⊥平面BCC1B1,
又BC1⊂平面BCC1B1,∴BD⊥BC1,
取DB的中点F,连接A1F,又A1D=A1B,
则A1F⊥BD,取DC1的中点M,连接FM,则FM∥BC1,∴FM⊥BD。
∴∠A1FM为二面角A1﹣BD﹣C1的平面角。
连接A1M,在△A1FM中,A1F=
FM=


取D1C1的中点H,连接A1H,HM,在Rt△A1HM中,
∵A1H=

∴cos∠A1FM=
∴二面角A1﹣BD﹣C1的余弦值为
知识点
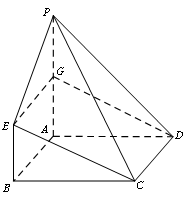
在如图所示的几何体中,四边形ABCD为正方形,
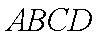

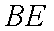

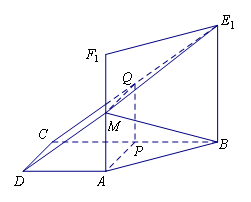
(1)求证:

(2)求PD与平面PCE所成角的正弦值;
(3)在棱
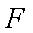


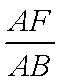
正确答案
见解析
解析
(1)设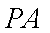
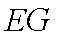

因为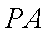
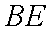
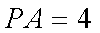
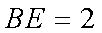
所以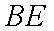

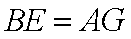
所以四边形
所以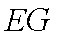


因为正方形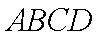
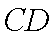


所以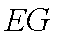
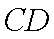
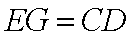
所以四边形
所以

因为
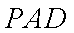
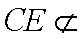
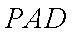
所以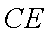
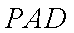
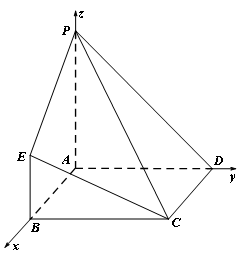
(2)如图建立空间坐标系,
则

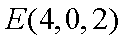

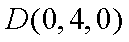
所以
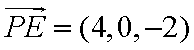

设平面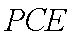
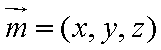
所以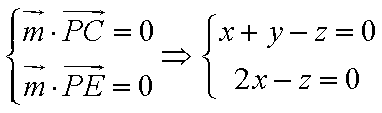
令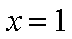
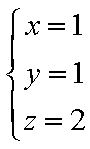
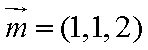
设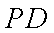
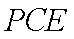
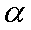
则
所以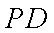

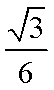
(3)依题意,可设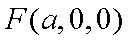
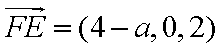
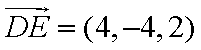
设平面

则
令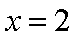
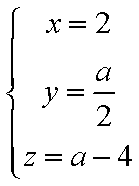
所以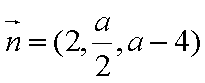
因为平面

所以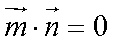
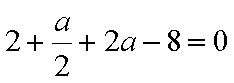
所以

所以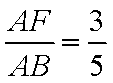
知识点
如图1,在直角梯形
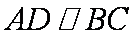
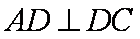
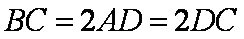

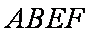
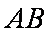
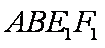
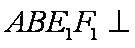
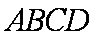

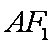
(1)求证: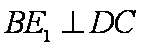
(2)求
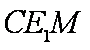
(3)判断直线
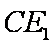
正确答案
见解析
解析
解析:
(1)证明:因为 四边形
所以 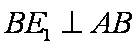
因为 平面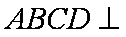


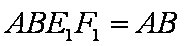

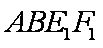
所以 
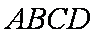
因为 

所以 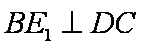
(2)解:如图,以点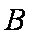


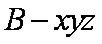
设
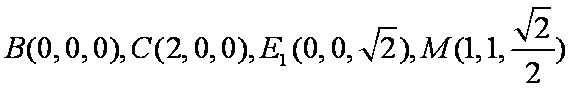
所以 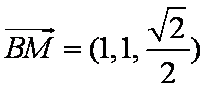

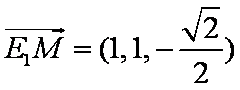
设平面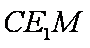

由
令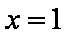

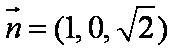
设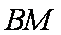
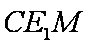

则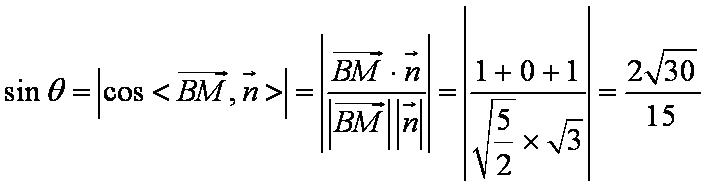
所以 


(3)解:直线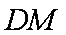

由题意得,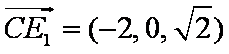
所以 
所以 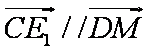
因为 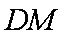
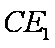
所以 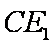

另解:直线

取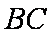
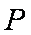
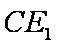
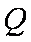



所以 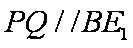

因为 
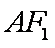

所以 

所以 

所以 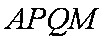
所以 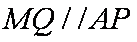

因为 四边形
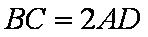
所以 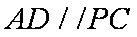

所以 四边形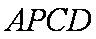
所以 
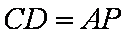
所以 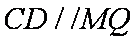

所以 
所以 

知识点
如图,AB是半圆O的直径,点C在半圆上,CD⊥AB,垂足为D,且AD=5DB,设∠COD=θ,则tanθ的值为 。
正确答案
解析
令圆O的半径为R,即OA=OB=OC=R
∵ AD=5DB∴OD=


由相交弦定理可得:CD2=AD•BD=
∴ CD=
∴ tanθ=
故答案为:
知识点
若函数


正确答案
解析
眼睛看到这个是三次函数,头脑中就闪现一般解题办法,求导解三次。这就是转化一念间
第一步识别条件: 继续识别条件:
第二步转化条件: 求导,把范围代入,看看导数的范围是啥,求出来的这个是切线的斜率。
第三步看问定向:倾斜角为
行了,画个正切函数图像,
知识点
若函数


正确答案
解析
眼睛看到这个是三次函数,头脑中就闪现一般解题办法,求导解三次。这就是转化一念间
第一步识别条件: 继续识别条件:
第二步转化条件: 求导,把范围代入,看看导数的范围是啥,求出来的这个是切线的斜率。
第三步看问定向: 倾斜角为
行了,画个正切函数图像,
第四步结论已出现:对照着找找角就行了
知识点
扫码查看完整答案与解析