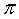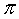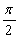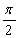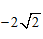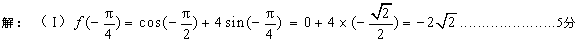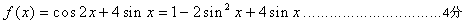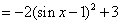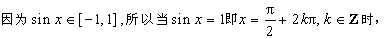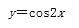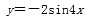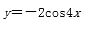- 三角函数的综合应用
- 共200题
曲线 



正确答案
6
解析
略
知识点
已知函数

(1)求函数
(2)如果



正确答案
(1)
解析
(1)

(2)


所以函数


故函数

知识点
若向量

正确答案
解析
略
知识点
已知函数
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)△ABC的内角分别是A,B,C,若f(A)=1,cosB=
正确答案
见解析。
解析
(1)由图象最高点得A=1,
由周期
当


因为


由图象可得

(2)由(1)可知, 






知识点
函数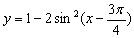
正确答案
解析
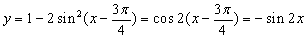

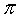
知识点
若
正确答案
解析
因


知识点
已知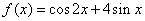
(1)求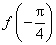
(2)求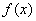

正确答案
(1)
(2)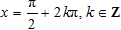
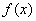
解析
(2)
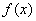
知识点
如右图所示,位于东海某岛的雷达观测站A,发现其北偏东 



正确答案
解析
略
知识点
在△

(1)求角
(2)若



正确答案
见解析。
解析
(1)由

所以原式化为
因为


因为

(2)由余弦定理,得

因为 

所以 
因为 

知识点
将函数y=2cos2x的图象向右平移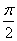
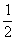
正确答案
解析
略
知识点
扫码查看完整答案与解析