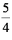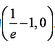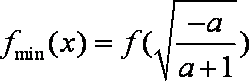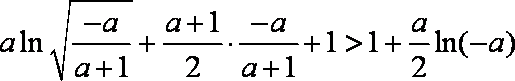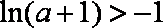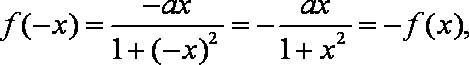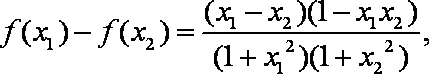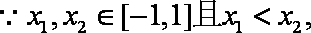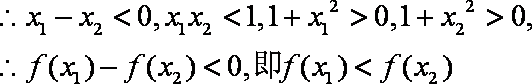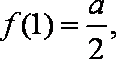- 三角函数的综合应用
- 共200题
已知函数
(1)求函数
(2)将函数



正确答案
见解析
解析
(1)
由


(2)由已知,
由



知识点
已知函数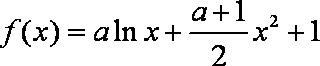
(1)当
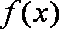
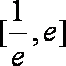
(2)讨论函数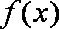
(3)当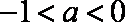
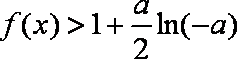
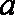
正确答案
(1)
(2)当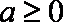
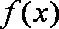
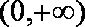
当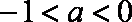
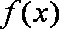
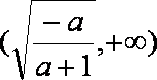
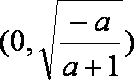
当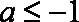
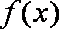
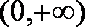
(3)
解析
(1)当

∴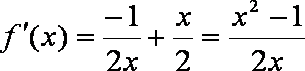
∵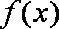
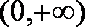
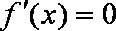
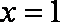
∴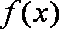
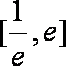
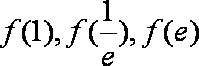
而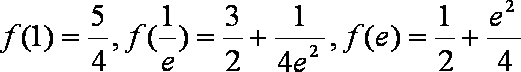
∴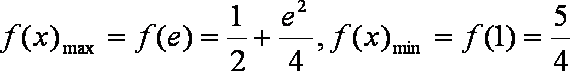
(2)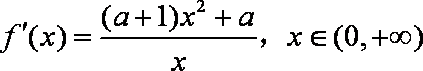
①当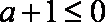
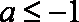
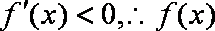
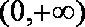
②当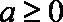
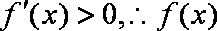
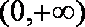
③当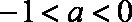

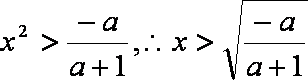
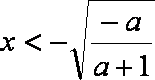
∴
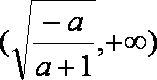
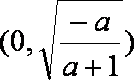
综上,
当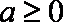
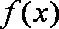
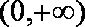
当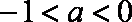
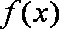
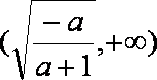
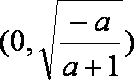
当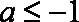
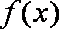
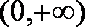
(3)由(2)知,当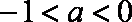
即原不等式等价于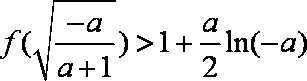
即
整理得
∴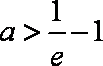
又∵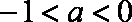
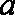

知识点
已知函数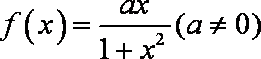
(1)判断并证明函数的奇偶性;
(2)当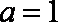
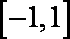
(3)求函数在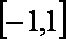
正确答案
见解析
解析
证明:(1)由题意,函数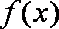
对任意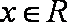
故f(x)在R上为奇函数;
(2)任取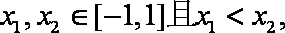
故f(x)在[-1,1]上为增函数;
(3)由(1)(2)可知:
①当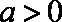

最小值为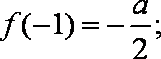
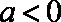
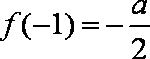
知识点
在△






(1)求证:
(2)求
正确答案
见解析
解析
解析:(1)由已知,
得
由基本不等式

所以

(2)
………………9分
由(1),


所以,


知识点
在

(1)求
(2)设






正确答案
见解析
解析
(1)设


(2)
设

知识点
已知函数

(1)求函数
(2)若

正确答案
见解析
解析
(1)由题设
由

故函数


(2)由

考察函数

于是
故

知识点










正确答案
解析
解析:由
于是
由已知得 
由

由①、②得

又

知识点
已知函数
(1)求
(2)若


正确答案
见解析
解析
(1)易得


所以


(2)由
又由
所以

此时,

知识点
若

正确答案
解析
∵ sin2θ+cos2θ=1,
∴ 便得出方程组
解这个关于sinθ与cosθ的2元2次方程组,
∴ 
故有
知识点
已知函数

(1)当


(2)如果函数




已知函数




正确答案
见解析
解析
解:(1)当

对于

∴
∴

(2)①在区间(1,+∞)上,函数

令

且


∵
(i)若



当



此时



当




(ii) 若


从而
要使

所以
又因为


综合可知

知识点
扫码查看完整答案与解析