几何证明选讲_章节学习

1

题型：简答题

|

简答题 · 10 分

选修4—1：几何证明选讲

如图6，圆O的直径，P是AB延长线上一点，BP=2 ,割线PCD交

圆O于点C，D，过点P作AP的垂线，交直线AC于点E，交直线AD于点F.

28. 当时，求的度数；

29.求的值.

第(1)小题正确答案及相关解析

正确答案

（1）；

解析

解：(Ⅰ) 连结BC，∵AB是圆O的直径 ∴则，

又，

，

∵；

考查方向

本题主要考查直径所对的圆周角是直角，四点共圆，切割线定理等知识，意在考查考生的逻辑推理能力和数形结合能力。

解题思路

找不到与之间的关系；

易错点

不会使用第（1）问的结论推导第（2）问；

第(2)小题正确答案及相关解析

正确答案

（2）24；

解析

(Ⅱ)由（Ⅰ）知，

∴D、C、E、F四点共圆，

∴,

∵PC、PA都是圆O的割线，∴，

∴=24.

考查方向

本题主要考查直径所对的圆周角是直角，四点共圆，切割线定理等知识，意在考查考生的逻辑推理能力和数形结合能力。

解题思路

无法发现D、C、E、F四点共圆导致不能使用割线定理。

易错点

不会使用第（1）问的结论推导第（2）问；

1

题型：简答题

|

简答题 · 10 分

选修4-1：几何证明选讲．

如图所示，已知与⊙相切，为切点，过点的割线交圆于两点，弦，相交于点，为上一点，且．

27.求证：；

28.若，求的长．

第(1)小题正确答案及相关解析

正确答案

见解析

解析

∵,∴∽,∴，又∵,∴, ∴,，∴∽， ∴， ∴，又∵，∴．

考查方向

本小题主要考查平面几何的证明，具体涉及到割线定理以及三角形相似等内容.重点考查考生对平面几何推理能力.

解题思路

先证明,再证，可证得

易错点

找不准三角形相似或全等的条件

第(2)小题正确答案及相关解析

正确答案

PA=

解析

∵, ∴ ，∵ ∴

由27题可知：，解得.∴． ∵是⊙的切线，∴，∴，解得．

考查方向

本小题主要考查平面几何的证明，具体涉及到割线定理以及三角形相似等内容.重点考查考生对平面几何推理能力.

解题思路

先综合题中条件及27中结论，解出EP=,BP=,再由切割线定理，解得PA=

易错点

找不准三角形相似或全等的条件

1

题型：简答题

|

简答题 · 14 分

等腰梯形中，∥，、交于点，平分，为梯形外接圆的切线，交的延长线于点．

27.求证：；

28.若，，，求的长．

第(1)小题正确答案及相关解析

正确答案

略；

解析

(1) 为圆的切线，平分

为圆的切线．-------------5分

考查方向

切割线定理、相似三角形的判定.

解题思路

根据切割线定理得，再证 ,即可得证.根据同弧对的圆周角相等，可得，进一步求即可.

易错点

难以找出相等的角，进而将边转化求长度.

第(2)小题正确答案及相关解析

正确答案

.

解析

与相似，

．-------------10分

考查方向

切割线定理、相似三角形的判定.

解题思路

根据切割线定理得，再证 ,即可得证.根据同弧对的圆周角相等，可得，进一步求即可.

易错点

难以找出相等的角，进而将边转化求长度.

1

题型：简答题

|

简答题 · 10 分

选修4-1：几何证明选讲

如图，AB是圆O的直径，点C在圆O上,延长BC到D使,过C作圆O的切线交AD于E.若,.

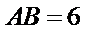
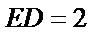
27.求证：;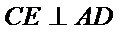

28.求BC的长.

第(1)小题正确答案及相关解析

正确答案

详见解析

解析

连接，因分别为的中点，所以,

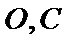
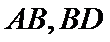
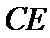
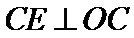
又为圆的切线，,所以

考查方向

圆切线的判定与性质

解题思路

作出半径，然后证明垂直关系

易错点

几何关系找不全，逻辑混乱

第(2)小题正确答案及相关解析

正确答案

详见解析

解析

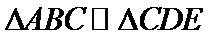
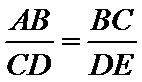
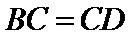
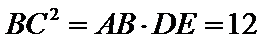
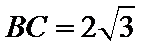
依题意易知,所以,又

,所以,从而.

考查方向

与圆有关的比例线段，相似三角形的性质和判定

解题思路

根据圆的比例线段关系，证明三角形相似，然后求出比例等式，进而求出线段的值

易错点

几何关系找不全，逻辑关系混乱

1

题型：简答题

|

简答题 · 10 分

正确答案

ＬＵＥ

知识点

圆的切线的性质定理的证明与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

正确答案

略

知识点

圆的切线的性质定理的证明与圆有关的比例线段

1

题型：单选题

|

单选题 · 5 分

7. 已知为圆的直径，于，为的中点，与相交于点，切线与的延长线交于点.若圆的半径为1，则的长为

A

B

C

D

正确答案

A

解析

因为DE为圆OD的直径，所以EC垂直于CD，因为圆O的半径为1，2ON=EC,所以,在直角三角形DEF中，

,所以选A

考查方向

与圆有关的比例线段

解题思路

利用射影定理求EF的长

易错点

对圆的切线的性质掌握不好

知识点

圆的切线的性质定理的证明

1

题型：简答题

|

简答题 · 10 分

AB是圆O的直径，D为圆O上一点，过D作圆O的切线交AB延长线于点C，若DA=DC，求证：AB=2BC。

正确答案

解析

（方法一）证明：连结OD，则：OD⊥DC，

又OA=OD，DA=DC，所以∠DAO=∠ODA=∠DCO，

∠DOC=∠DAO+∠ODA=2∠DCO，

所以∠DCO=300，∠DOC=600，

所以OC=2OD，即OB=BC=OD=OA，所以AB=2BC。

（方法二）证明：连结OD、BD。

因为AB是圆O的直径，所以∠ADB=900，AB=2 OB。

因为DC 是圆O的切线，所以∠CDO=900。

又因为DA=DC，所以∠DAC=∠DCA，

于是△ADB≌△CDO，从而AB=CO。

即2OB=OB+BC，得OB=BC。

故AB=2BC。

知识点

圆的切线的判定定理的证明弦切角

1

题型：简答题

|

简答题 · 10 分

请在22、23、24三题中任选一题作答，如果多做，则按所做的第一题计分。

22．选修4-1：几何证明选讲

如图，切于点，直线AO交于，两点，，垂足为．

（1）证明：；

（2）若，，求的直径．

23.选修4-4：坐标系与参数方程

在直角坐标系中，直线的参数方程为（为参数）．以原点为极点，轴正半轴为极轴建立极坐标系，的极坐标方程为．

（1）写出的直角坐标方程；

（2）为直线上一动点，当到圆心的距离最小时，求的直角坐标．

24.选修4-5：不等式选讲

已知关于的不等式的解集为．

（1）求实数，的值；

（2）求的最大值．

正确答案

22.（1）因为DE为圆O的直径，则，

又BCDE，所以CBD+EDB=90°，从而CBD=BED.

又AB切圆O于点B，得DAB=BED，所以CBD=DBA.

（2）由（1）知BD平分CBA，则,又，从而，

所以，所以.

由切割线定理得，即=6，

故DE=AE-AD=3，即圆O的直径为3.

23.（1）由，

从而有.

（2）设,则，

故当t=0时，|PC|取最小值，此时P点的直角坐标为（3，0）.

24.（1）由，得

则解得,

（2）

当且仅当，即时等号成立，

故.

解析

解析已在路上飞奔，马上就到！

知识点

圆的切线的性质定理的证明与圆有关的比例线段

1

题型：简答题

|

简答题 · 10 分

请考生在22、23、24题中任选一题作答，如果多做，则按所做的第一题计分，作答时请写清题号。

22.（本小题满分10分）

选修4—1：几何证明选讲

如图，为等腰三角形内一点，圆与的底边交于、两点与底边上的高交于点，与、分别相切于、两点.

（Ⅰ）证明：；

（Ⅱ）若等于的半径，且，求四边形的面积.

23.（本小题满分10分）选修4-4：坐标系与参数方程

在直角坐标系中，曲线（为参数，），其中，在以为极点，轴正半轴为极轴的极坐标系中，曲线，曲线.

（Ⅰ）.求与交点的直角坐标；

（Ⅱ）.若与相交于点，与相交于点，求的最大值.

24.（本小题满分10分）选修4-5不等式选讲

设均为正数，且，证明：

（Ⅰ）若，则；

（Ⅱ）是的充要条件.

正确答案

22.

（Ⅰ）详见解析；（Ⅱ）.

试题分析：（Ⅰ）由已知得，欲证明，只需证明，由切线长定理可得，故只需证明是角平分线即可；（Ⅱ）连接，，在中，易求得，故和都是等边三角形，求得其边长，进而可求其面积.四边形的面积为两个等边三角形面积之差.

试题（Ⅰ）由于是等腰三角形，，所以是的平分线.又因为分别与、相切于、两点，所以，故.从而.

（Ⅱ）由（Ⅰ）知，,，故是的垂直平分线，又是的弦，所以在上.连接，，则.由等于的半径得，所以.所以和都是等边三角形.因为，所以，.

因为，，所以.于是，.所以四边形的面积.

23.

（Ⅰ）和；（Ⅱ）.

试题分析：（Ⅰ）将曲线与的极坐标方程化为直角坐标方程，联立求交点，得其交点的直角坐标，也可以直接联立极坐标方程，求得交点的极坐标，再化为直角坐标；（Ⅱ）分别联立与和与的极坐标方程，求得的极坐标，由极径的概念将表示，转化为三角函数的最大值问题处理.

试题（Ⅰ）曲线的直角坐标方程为，曲线的直角坐标方程为.联立解得或所以与交点的直角坐标为和.

（Ⅱ）曲线的极坐标方程为，其中.因此得到极坐标为，的极坐标为.所以，当时，取得最大值，最大值为.

24.

（Ⅰ）详见解析；（Ⅱ）详见解析.

解析

解析已在路上飞奔，马上就到！

知识点

圆的切线的性质定理的证明与圆有关的比例线段

热门试卷

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点