- 几何证明选讲
- 共247题
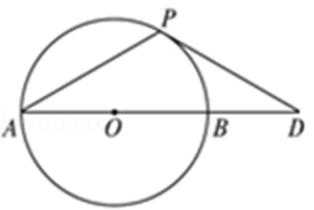
如图,过圆











(1)求
(2)求证:
正确答案
见解析
解析
(1)延长



则
又

又

根据切割线定理得
(2)证明:过



从而有
所以

知识点
如图,过圆E外一点A作一条直线与圆E交B,C两点,且AB=

(1)求AF的长;
(2)求证:AD=3ED。
正确答案
见解析。
解析
(1) 延长




又


又

所以根据切割线定理

(2)过




从而有

知识点
如图,BA是⊙O的直径,AD是切线,BF、BD是割线,
求证:BE•BF=BC•BD
正确答案
见解析
解析
证法一:
连接CE,过B作⊙O的切线BG,则BG∥AD
∴∠GBC=∠FDB,又∠GBC=∠CEB ∴∠CEB=∠FDB
又∠CBE是△BCE和△BDF的公共角 ∴△BCE∽△BDF ∴
证法二:连续AC、AE,∵AB是直径,AC是切线 ∴AB⊥AD,AC⊥BD,AE⊥BF
由射线定理有AB2=BC•BD,AB2=BE•BF ∴BE•BF=BC•BD
知识点
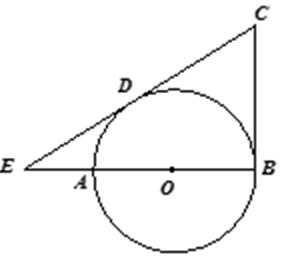
已知PQ与圆O相切于点A,直线PBC交圆于B,C两点,D是圆上一点,且AB∥CD,DC的延长线交PQ于点Q。
(1)求证:AC2=CQ·AB;
(2)若AQ=2AP,AB=
正确答案
见解析
解析
解析:
(1)
(2)

又因为

知识点
如图,已知PE切⊙O于点E,割线PBA交⊙O于A、B两点,∠APE的平分线和AE、BE分别交于点C、D.求证:
(1)CE=DE;
(2)
正确答案
见解析
解析
(1)证明:





(2)证明:


同理


知识点
如图,圆周角







(1)求证:
(2)若





正确答案
见解析
解析
(1)证明:因为∠EDC=∠DAC,∠DAC=∠DAB,∠DAB=∠DCB,
所以∠EDC=∠DCB,
所以BC∥DE,
(2)解:因为D,E,C,F四点共圆,所以∠CFA=∠CED
由(1)知∠ACF=∠CED,所以∠
设∠DAC=∠DAB=x,
因为
所以∠CFA=∠FBA+∠FAB=3x,
在等腰△ACF中,π=∠CFA+∠ACF+∠CAF=7x,

知识点
如图所示,已知PA是⊙O相切,A为切点,PBC为割线,弦CD//AP,AD、BC相交于E点,F为CE上一点,且
(1)求证:A、P、D、F四点共圆;
(2)若AE·ED=24,DE=EB=4,求PA的长。
正确答案
见解析
解析
解析: (1)证明:
又


又

所以
(2)解:由(1)及相交弦定理得
又

由切割线定理得
所以
知识点
已知




圆




(1)证明:
(2)若

正确答案
见解析
解析
(1)∵ PA是切线,AB是弦,∴ ∠BAP=∠C,
又 ∵ ∠APD=∠CPE,∴ ∠BAP+∠APD=∠C+∠CPE,∵ ∠ADE=∠BAP+∠APD,
∠AED=∠C+∠CPE,∴ ∠ADE=∠AED。
(2)由(1)知∠BAP=∠C,又 ∵ ∠APC=∠BPA, ∴ △APC∽△BPA, ∴
∵ AC=AP, ∴ ∠APC=∠C=∠BAP,由三角形内角和定理可知,∠APC+∠C+∠CAP=180°,
∵ BC是圆O的直径,∴ ∠BAC=90°, ∴ ∠APC+∠C+∠BAP=180°-90°=90°,
∴ ∠C=∠APC=∠BAP=




知识点
15.如图,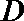
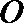
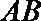
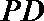
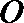
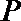
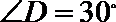
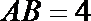
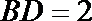
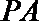
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如图,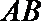
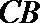
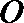
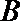
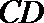
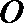
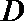
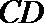
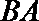

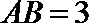
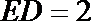

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析