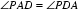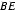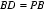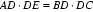- 几何证明选讲
- 共247题
如图,M是平行四边形ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F,若AD=3AE,则AF:FC= 。
正确答案
1:4
解析
如图所示,设直线l交CD的延长线于点N。
∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD。
∵M是边AB的中点,∴
∴

故答案为1:4。
知识点
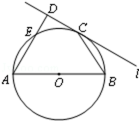
如图,⊙O的半径OB垂直于直径AC,M为AO上一点,BM的延长线交⊙O于N,过N点的切线交CA的延长线于P。
(1)求证:PM2=PA•PC;
(2)若⊙O的半径为2

正确答案
见解析
解析
(1)证明:连接ON,因为PN切⊙O于N,
∴∠ONP=90°,
∴∠ONB+∠BNP=90°
∵OB=ON,
∴∠OBN=∠ONB
因为OB⊥AC于O,
∴∠OBN+∠BMO=90°,
故∠BNP=∠BMO=∠PMN,PM=PN
∴PM2=PN2=PA•PC
(2)∵OM=2,BO=2
∵BM•MN=CM•MA=(

∴MN=2
知识点
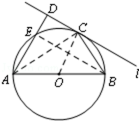
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使得CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F,求证BE平分∠ABC。
正确答案
见解析。
解析
∵CD=AC,
∴∠D=∠CAD。
∵AB=AC,
∴∠ABC=∠ACB。
∵∠EBC=∠CAD,
∴∠EBC=∠D。
∵∠ABC=∠ABE+∠EBC,∠ACB=∠D+∠CAD。
∴∠ABE=∠EBC,
即BE平分∠ABC。
知识点
圆的两弦AB、CD交于点F,从F点引BC的平行线和直线AD交于P,再从P引这个圆的切线,切点是Q。
求证:PF=PQ。
正确答案
见解析。
解析
因为A,B,C,D四点共圆,所以ADF=ABC,
因为PF∥BC,所以AFP=ABC,所以AFP=FQP,
又因为APF=FPA,
所以△APF∽△FPQ,
所以

因为PQ与圆相切,所以
所以
知识点
如图,





(1)证明:
(2)证明:
正确答案
见解析
解析
(1)由切割线定理知

(2)由


又四边形GEDF四点共圆,所以
故
知识点
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,求线段AE的长。
正确答案
见解析
解析
连接OC,BE,AC,则BE⊥AE。
∵BC=4,∴OB=OC=BC=4,即△OBC为正三角形,
∴∠CBO=∠COB=60°。
又直线l切⊙O与C,∴OC⊥l,
∵AD⊥l,∴AD∥OC。
∴∠EAB=∠COB=60°。
在Rt△BAE中,∴∠EBA=30°,
∴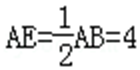
知识点
如图,






求证:(1)
(2)
正确答案
见解析
解析
证明:(1)

(2)








知识点
如图,以





另一个交点



(1)证明

(2)若

正确答案
见解析
解析
(1)证明:连接

∴

∴△


∵



∴

∴

(2)解:∵





∵




∴⊙
知识点
如图,














(1)求证:
(2)若

正确答案
见解析。
解析
(1)证明:连结




在

又∵
∴
(2)∵
∵


又因为
∴
知识点
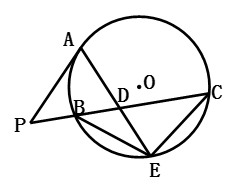
22.如图,
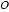
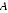
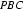
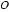
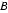
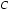
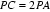
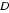
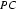
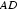
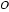
证明:(Ⅰ)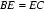
(Ⅱ)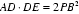
正确答案
略
解析
试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
(Ⅰ)证明:连接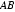
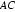

因为: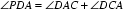
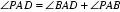
由弦切角等于同弦所对的圆周角: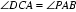
所以: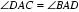

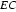
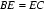
(Ⅱ)由切割线定理得: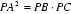
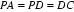
所以: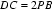
由相交弦定理得:
所以: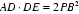
考查方向
本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
解题思路
本题考查平面几何的知识,解题步骤如下:
1、利用圆的相关定理证明。
2、原来切割线定理和相交弦定理证明。
易错点
相关的定理容易混用。
知识点
扫码查看完整答案与解析