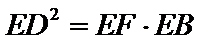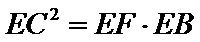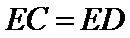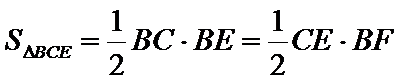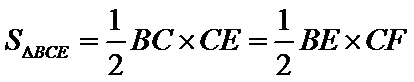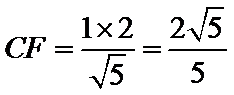- 几何证明选讲
- 共247题
请考生在以下3题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
【选修4-1:几何证明选讲】(请回答28、29题)
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,
【选修4—4:坐标系与参数方程】(请回答30、31题)
在直角坐标系x

在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=
【选修4—5:不等式选讲】(请回答32、33题)
已知函数
28.证明:直线AB与
29.点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
30.说明C1是哪一种曲线,并将C1的方程化为极坐标方程;
31.直线C3的极坐标方程为


32.在答题卡第(24)题图中画出
33.求不等式
正确答案
见解析
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
设


因为


在






考查方向
解题思路
先证明

易错点
对相关定理不熟悉导致本题失分。
正确答案
见解析
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
因为





由已知得




同理可证,

考查方向
解题思路
(2)利用四点共圆,作直线

易错点
对相关定理不熟悉导致本题失分。
正确答案
圆,
解析
试题分析:本题属于坐标系与参数方程的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:


∴
∴


∵
∴

考查方向
解题思路
直接利用互化公式即可求出极坐标方程;
易错点
不能熟记极坐标方程与参数方程的互化公式及应用导致本题出错。
正确答案
1
解析
试题分析:本题属于坐标系与参数方程的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:








①—②得:
∴
考查方向
解题思路
把直线的参数方程化为普通方程,即可求解.
易错点
不能熟记极坐标方程与参数方程的互化公式及应用导致本题出错。
正确答案
解析
试题分析:本题属于不等式的选讲内容,不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等,解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式,属于简单题,只要掌握相关不等式的知识,即可解决本题,解析如下:
如图所示:
考查方向
解题思路
先将函数写成分段函数,然后作图;
易错点
忽略不等式的解集一定要写出集合形式导致丢分。
正确答案
解析
试题分析:本题属于不等式的选讲内容,不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等,解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式,属于简单题,只要掌握相关不等式的知识,即可解决本题,解析如下:
当


当



当



综上,


考查方向
解题思路
用零点分区间法分类讨论,然后取并集.
易错点
忽略不等式的解集一定要写出集合形式导致丢分。
选修4-1:几何证明选讲
如图,






28.求证:
29.求证:
正确答案
详见解题过程;
解析
试题分析:本题属于平面几何的基本问题,由圆的性质直接导出角关系。∵




考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
正确答案
详见解题过程
解析
试题分析:本题属于平面几何的基本问题,由相似关系去证所证。连接





考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
选修4—1,几何证明选讲
圆












28.求证:△

29.如果

正确答案
见解析
解析
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
正确答案
见解析
解析





考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
选修4—1:几何证明选讲
如图,
















27.
28.
正确答案
(1)略;
解析
【证明】(Ⅰ)由直线

由AB为⊙O的直径,得AE⊥EB,从而∠EAB+∠EBF=
又EF⊥AB,得∠FEB+∠EBF=
考查方向
解题思路
先根据切割线定理求出

易错点
找不到角之间的等量关系导致无法证明;
正确答案
(2)略
解析
(Ⅱ)由BC⊥CE,EF⊥AB,∠FEB=∠CEB,BE是公共边,得Rt△BCE≌Rt△BFE,
所以BC=BF.
类似可证,Rt△ADE≌Rt△AFE,得AD=AF.
又在Rt△

考查方向
解题思路
先证明
易错点
找不到中间联系的量AF·BF导致证明无法进行下去。
如图,
27.若

28.若E为上

正确答案
见解析
解析
∵PA交圆O于B,A PC交圆O于C,D,
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
正确答案
见解析
解析
连接EO CO,∵








考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准
【选修4-1:几何证明选讲】
如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,
27.求证:BC=CD;
28.过点C作圆O的切线交AD延长线于点H,若AB=4,DH =1,求AD的长.
正确答案
(1)BC=CD;
解析
(1)由题意知

又∵



由


∴

∴


考查方向
解题思路
(1)通过弧长相等得出线段相等;(2)通过圆的切割线定理计算AD的长。
易错点
对圆的切割线定理的灵活运用。
正确答案
(2)AD=2
解析
(2)∵

又∵


∴


由(1)知


∴

由切割线定理,得


考查方向
解题思路
(1)通过弧长相等得出线段相等;(2)通过圆的切割线定理计算AD的长。
易错点
对圆的切割线定理的灵活运用。
14.如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE:ED=2:1,则BE=_______.
正确答案
2
解析
首先由切割线定理得






考查方向
解题思路
平面几何问题主要涉及三角形全等,三角形相似,四点共圆,圆中的有关比例线段(相关定理)等知识,本题中有圆的切线,圆的割线,圆的相交弦,由圆的切割线定理和相交弦定理就可以得到题中有关线段的关系.
易错点
平面几何有关性质的综合应用
知识点
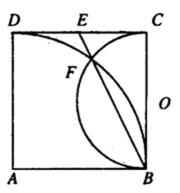
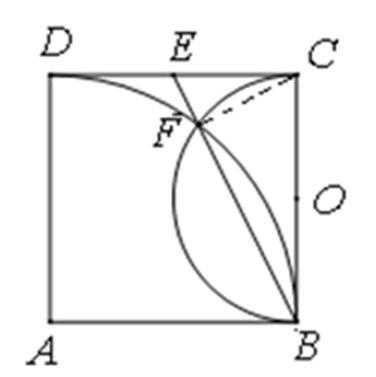
如图,正方形ABCD边长为2,以A为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F,连结BF并延长交CD于点E.
27.求证:E为CD的中点;
28.求EF·FB的值.
正确答案
见解析
解析
解:(Ⅰ)由题可知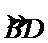
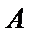
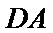
∴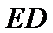
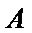
依据切割线定理得
∵圆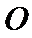
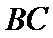
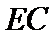
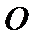
同样依据切割线定理得
故
∴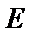
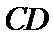
考查方向
解题思路
本题解题思路
1)借助圆的切割定理得出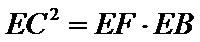
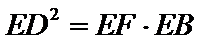
2)借助等面积求解FC,使用射影定理得到第二问
易错点
本题易错cd是两圆的切线,
正确答案
见解析
解析
解:
(Ⅱ)连结
∵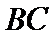
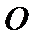
∴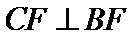
得
又在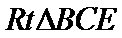
考查方向
解题思路
本题解题思路
1)借助圆的切割定理得出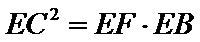
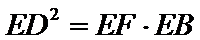
2)借助等面积求解FC,使用射影定理得到第二问
易错点
本题易错cd是两圆的切线,
选修4-1:几何证明选讲
如图,过圆













27.求
28.求
正确答案
3;
解析
延长











考查方向
解题思路
第一问由切割线定理可得;
易错点
三角形相似容易找错,切割线定理用不熟练。
正确答案
解析
过







考查方向
解题思路
第二问将两条线段归到两个相似三角形中,用相似得到比例关系。
易错点
三角形相似容易找错,切割线定理用不熟练。
8.如图,以











正确答案
解析
连接BE,由BC为直径知













考查方向
解题思路
1.先根据射影定理求出


易错点
1.看不出AB、BE和AE之间的关系;2.不会利用割线定理找关系求解。
知识点
扫码查看完整答案与解析