- 推理与证明
- 共88题
有三张卡片,分别写有1和2,1和3,2和3。甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是 。
正确答案
1和3
知识点
10.在实数集

在平面向量集








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.对大于或等于2的自然数m的n次幂进行如图的方式“分裂”,仿此,52的“分裂”中最大的数是___________,若m3的“分裂”中最小的数是211,则m的值为___________。
正确答案
9,15
解析
解析已在路上飞奔,马上就到!
知识点
15.今年国庆节期间,甲、乙、丙、丁四位驴友准备自驾游,四人筛选了A,B,C,D,E五个景点,由于时间关系只能去一个景点,于是他们商量去哪一个景点:
甲说:只要不去D就行;
乙说:B,C,D,E都行;
丙说:我喜欢B,但只要不去C就行;
丁说:除了E之外其他都可以.
据此推断,他们四人共同去的景点是________.
正确答案
B
解析
根据甲说的排除D;根据乙说的排除A;根据丙说的排除C;根据丁说的排除E,由此可知他们四人共同去的景点是B
知识点
4.对大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”,23


正确答案
解析
由题意知,自然数m的三次幂可用m个连续奇数进行“分裂”,把1算在内,从13到m3用从1开始的连续奇数共有1+2+3+…+m=


知识点
11.设m,n∈R,定义运算“

m


若正数m,n,a,b满足mn≥4,a+b≤4,则( ).
正确答案
解析
根据题意,知m

因为4≤mn≤(




知识点
29.在平面直角坐标系





(1)设椭圆




(2)设点









(3)已知直线

















正确答案
(1)
(2)
(3)
(1)由点

由题意

又

(也可以先求出

(2)假设存在实数
由题意
于是


只要
故存在实数



(学生通过联想,判断直线



(3)设




又

所以
综上
解析
试题分析:本题属于圆锥曲线中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求
(2)要注意对参数的讨论.
考查方向
本题考查了直线与椭圆的位置关系,属于高考中的高频考点
解题思路
本题考查圆锥曲线与直线的位置关系,解题步骤如下:
1、利用新定义求解。
2、联立直线与椭圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
设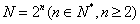
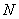
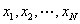

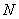
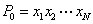

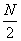
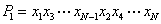
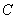
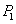
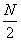
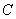
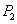
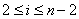
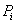
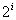
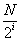
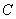
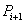
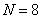
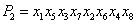
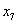
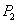
(1)当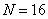
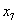
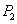
(2)当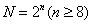
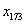
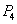
正确答案
(1)6
(2)
解析
(1)当N=16时,
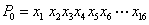
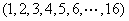
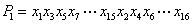
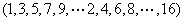
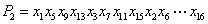
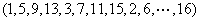
(2)方法同(1),归纳推理知x173位于P4中的第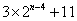
知识点
12.对于正整数n和m(m<n)定义

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 把正整数排列成如图甲的三角形数阵,然后擦去第偶数行的奇数和第奇数行中的偶数,得到如图乙的三角数阵,再把图乙中的数按从小到大的顺序排成一列,得到数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列






















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知集合M={



①M={
②M={
③M={
④M={
其中是“垂直对点集”的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.由
①正方形的对角线相等;
②平行四边形的对角线相等;
③正方形是平行四边形,
根据“三段论”推理出一个结论,则这个结论是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
设



(1)数表
(2) 数表

(3)对由



能否经过有限次“操作”以后,使得到的数表每行的各数之
和与每列的各数之和均为非负整数?请说明理由.
正确答案
见解析
解析
(1)解:法1:
法2:
法3:
…………………3分
(2)每一列所有数之和分别为2,0,

①如果首先操作第三列,则
则第一行之和为

这两个数中,必须有一个为负数,另外一个为非负数,
所以 
当
此时每列之和分别为
必有
当
此时第4列和为负,不符合题意. …………………6分
② 如果首先操作第一行
则每一列之和分别为


当
当


所以此时必须有


经检验,

综上:
(3)能经过有限次操作以后,使得得到的数表所有的行和与所有的列和均为非负实数。证明如下:
记数表中第











按要求操作一次时,使该行的行和(或该列的列和)由负变正,都会引起






知识点
正偶数列有一个有趣的现象:
①2+4=6
②8+10 +12=14+16;
③18+20+22+24=26+28+30,…
按照这样的规律,则2016在第 个等式中。
正确答案
31
解析
略
知识点
扫码查看完整答案与解析