- 三角恒等变换
- 共864题
15.已知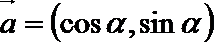

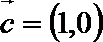
(1)若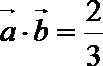
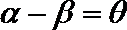

(2)若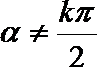

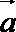
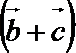
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在△ABC中,角A,B,C的对边分别为a,b,c,且
(1)求角
(2)若角




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)求函数
(2)求函数
(3)求函数
正确答案
解:
(1)

(2)

(3)令
则
所以函数

解析
解析已在路上飞奔,马上就到!
知识点
6.△ABC的三个内角以弧度度量,设M=Acos B+sin Acos C,则( ).
正确答案
解析
(1)△ABC为锐角三角形时,M>0.
(2)△ABC为直角三角形时,M>0.
(3)△ABC为钝角三角形时,①若A>
②若B>
③若C>
由于A>sin A,因此M>0.
由(1)、(2)、(3)知答案为A.
知识点
20.把函




(1)求a的最小值;
(2)当a取最小值,求函数

正确答案
(1)
∴

∴


(2)由(1)知
即
解析
解析已在路上飞奔,马上就到!
知识点
17.已知向量

(1)求出

(2)

(3)设



正确答案
(1)
其振幅为

(2)可由



(3)由
∵ 


∴
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
已知f(x)=sin x+cos x+|sin x-cos x|,
当sin x≥cos x,
即
f(x)=2sin x,
此时,f(x)的取值范围为
当sin x<cos x,
即
f(x)=2cos x,
此时,f(x)的取值范围为
所以函数f(x)=sin x+cos x+|sin x-cos x|的最大值与最小值分别为2和
知识点
11.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知

正确答案
解析
-(cos2x-sin2x)=-2cos(2x+




考查方向
解题思路
本题考查运用辅助角公式求辅助角,解题步骤如下:
先用辅助角公式得-2cos(2x+



易错点
本题必须注意
知识点
4.函数
正确答案
解析
∵
而∴
∴
考查方向
本题主要考查三角化简,是容易题.
解题思路
先逆用二倍角公式,然后用辅助角公式,最后利用三角函数的有界性求得函数的最小值.
易错点
三角公式很多,容易混淆公式的使用;逆用公式易出错.
知识点
扫码查看完整答案与解析