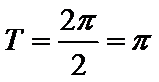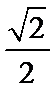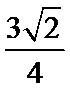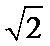- 三角恒等变换
- 共864题
10.已知

正确答案

解析
化简的
则
解不等式
∴单调递减区间为
考查方向
解题思路
1、由三角函数公式化简可得

易错点
主要易错于三角函数恒等变换出错
知识点
设△






已知
16.求
17.若

正确答案
解析
解:由


∴

考查方向
解题思路
可直接将题中的等式关系,用正弦定理将边的关系转成角的关系,再结合两角和公式,求出角A
易错点
问题容易在利用均值不等式放缩时出错
正确答案
解析
解:由

∴
∴
∴

又由题意知:
故:
考查方向
解题思路
可根据余弦定理, 得到b,c关系的等式, 再利用均值不等式进行合理缩放,可求出b+c取值范围
易错点
问题容易在利用均值不等式放缩时出错
2.函数f(x)= 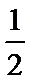
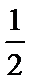
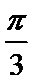
正确答案
解析
因为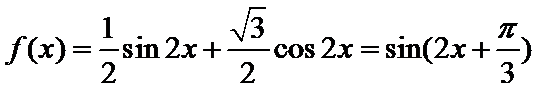
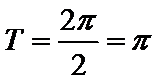
故A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
先化简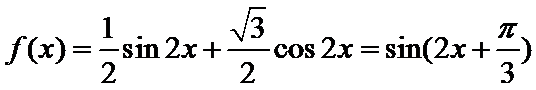
故A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
对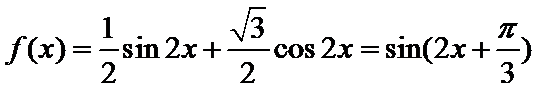
知识点
在△ABC中,角A,B,C的对边分别为


16.求角A的大小;
17.设函数

正确答案
(1)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(1)在


在△ABC中,因为

所以


考查方向
解题思路
1)第一问中利用余弦定理得到

2)第二问中用倍角公式,和差公式可得
易错点
1)第一问中用余弦定理得到


2)第二问中用倍角公式,和差公式可得
正确答案
(2)
解析
试题分析:本题属于三角函数的基本问题,题目的难度是逐渐由易到难,(1)直接按步骤来求,(2)要注意三角恒等变换的正确性;
(2)由(1)得
令
即函数
考查方向
解题思路
1)第一问中利用余弦定理得到

2)第二问中用倍角公式,和差公式可得
易错点
1)第一问中用余弦定理得到


2)第二问中用倍角公式,和差公式可得
3. 已知


正确答案
解析




所以

考查方向
解题思路
1.先根据题中条件求出角
易错点
1.利用诱导公式在化简时出错;2.对于特殊角的三角函数值记忆出错。
知识点
4.在



正确答案
解析
由题意及正弦定理得




考查方向
解题思路
1.先根据正弦定理将角化为边;2.利用余弦定理求出角C即可。
易错点
1.不知道该将

知识点
已知函数
15.确定
16.求函数

正确答案
(1)2;
解析
(Ⅰ)
因为最小正周期
所以
考查方向
解题思路
先将函数化简为一个角的一个三角函数的形式,然后利用周期即可求得答案;
易错点

正确答案
(2)最大值为1,最小值为
解析
(Ⅱ)






故函数


考查方向
解题思路
先判断函数的增减性,然后即可求得最大值和最小值。
易错点
直接将端点值带入求解得到值域,没有考虑到函数的单调出错。
11.已知函数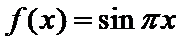
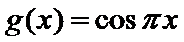
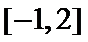
正确答案
解析
由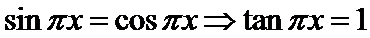
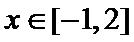
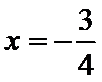
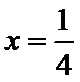
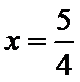
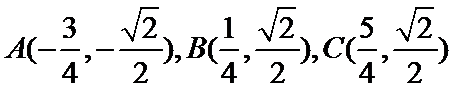
故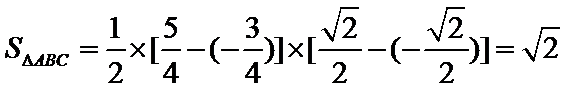
考查方向
解题思路
1.先根据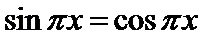
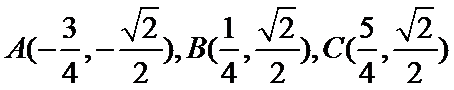
易错点
1.不会结合图像求出A,B,C的坐标;2.不会做函数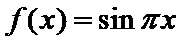
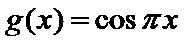
知识点
4.已知



正确答案
解析
函数图像的一个最高点与其相邻的一个最低点的距离为5,可求得水平距离为3,所以周期为6,则

考查方向
解题思路
先求周期为6, 再由公式求出
易错点
容易将题中的距离理解为水平距离,而错选C
知识点
9.已知角



正确答案
-2,
解析
由三角函数定义,可知角











考查方向
解题思路
根据三角函数的定义,解出tan
易错点
定义理解不到位,公式应用错误
知识点
扫码查看完整答案与解析