- 三角恒等变换
- 共864题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知函数f(x)=ax3-3x2+1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是( )
正确答案
解析
当a=0时,f(x)=-3x2+1,存在两个零点,不符合题意,故a≠0.
由f′(x)=3ax2-6x=0,得x=0或x=.
若a<0,则函数f(x)的极大值点为x=0,且f(x)极大值=f(0)=1,极小值点为x=,且f(x)极小值=f=,此时只需>0,即可解得a<-2;
若a>0,则f(x)极大值=f(0)=1>0,此时函数f(x)一定存在小于零的零点,不符合题意。
综上可知,实数a的取值范围为(-∞,-2)。
知识点
一个正三棱柱的侧棱长和底面边长相等,体积为2
正确答案
2
解析
设正三棱柱的侧棱长为:a,由题意可知,



故答案为:2
知识点
设集合

正确答案
解析
由A≠


由题意知,若A∩B≠
则有(1)当2m+1<2,即m<
圆心(2,0)到直线x+y=2m+1的距离为d1=
化简得2m2-4m+1≤0,
解得1-

所以1-

(2)当2m≤2≤2m+1,即

(3)当2m>2,即m>1时,
圆心(2,0)到直线x+y=2m的距离为d2=
化简得m2-4m+2≤0,
解得2-

所以1<m≤2+
综上可知:满足题意的m的取值范围为

知识点
从一副混合后的扑克牌(52张)中随机抽取1张,事件A为“抽得红桃K”,事件B为“抽得为黑桃”,则概率P(A
正确答案
解析
考查互斥事件概率公式 P(A
知识点
如图,为保护河上古桥OA,规划建一座新桥BC,同时设立一个圆形保护区,规划要求:新桥BC与河岸AB垂直;保护区的边界为圆心M在线段OA上并与BC相切的圆,且古桥两端O和A到该圆上任意一点的距离均不少于80m,经测量,点A位于点O正北方向60m处,点C位于点O正东方向170m处(OC为河岸),
(1)求新桥BC的长;
(2)当OM多长时,圆形保护区的面积最大?
正确答案
见解析。
解析
解法一:
如图,以O为坐标原点,OC所在直线为x轴,建立平面直角坐标系xOy.
由条件知A(0, 60),C(170, 0),
直线BC的斜率k BC=-tan∠BCO=-
又因为AB⊥BC,所以直线AB的斜率k AB=
设点B的坐标为(a,b),则k BC=
k AB=
解得a=80,b=120. 所以BC=
因此新桥BC的长是150 m.
(2)设保护区的边界圆M的半径为r m,OM=d m,(0≤d≤60)。
由条件知,直线BC的方程为
由于圆M与直线BC相切,故点M(0,d)到直线BC的距离是r,
即
因为O和A到圆M上任意一点的距离均不少于80 m,
所以

故当d=10时,
所以当OM = 10 m时,圆形保护区的面积最大。
知识点
不等式
正确答案
(-4,2)
解析
考查分式不等式的解法
知识点
某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素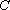
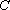
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
正确答案
见解析。
解析
设为该儿童分别预订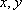

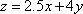
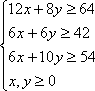
作直线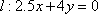
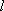
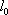


由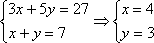
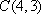
此时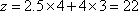
答: 午餐和晚餐分别预定4个单位和3个单位,花费最少z=22元。
知识点
扫码查看完整答案与解析