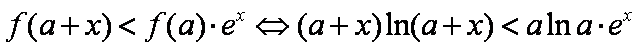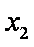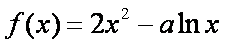- 三角恒等变换
- 共864题
已知函数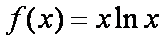
(1)讨论函数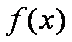
(2)对于任意正实数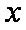
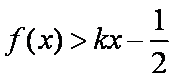
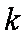
(3)是否存在最小的正常数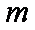
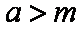
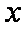
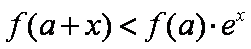
正确答案
见解析。
解析
(1)令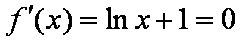
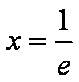
当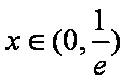
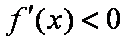
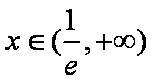
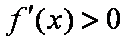
所以函数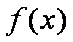
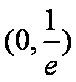
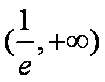
(2)由于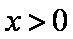
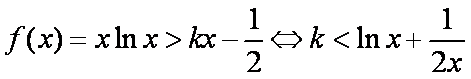
构造函数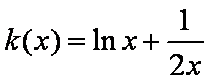
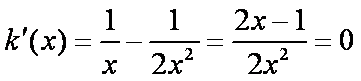
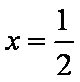
当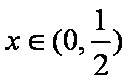
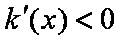
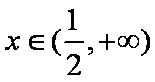
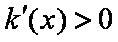
所以函数在点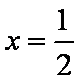
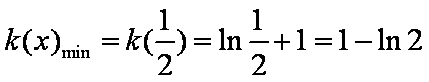
因此所求的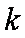
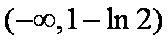
(3)结论:这样的最小正常数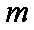
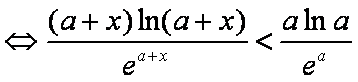
构造函数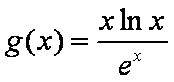
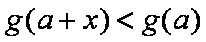
对于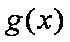
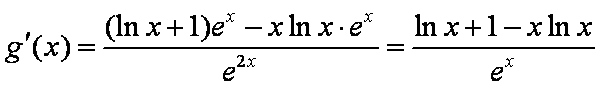
令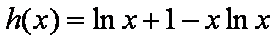

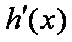
又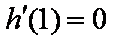
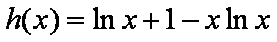
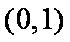
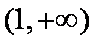
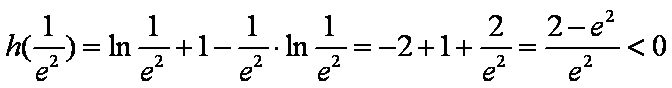
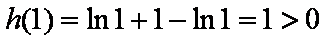
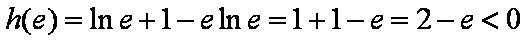
所以函数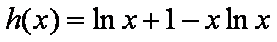
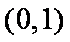
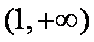
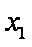
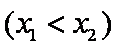
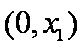
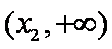
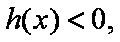
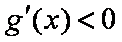
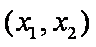
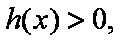
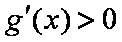
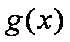
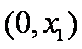
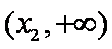
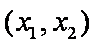
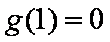
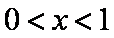
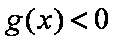

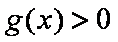
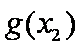
题目要找的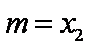
当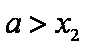
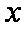
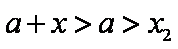
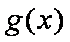
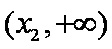
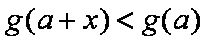

当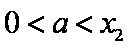
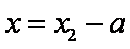

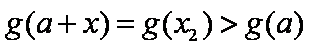
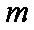
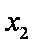
综合可知,题目所要寻求的最小正常数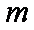
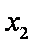
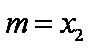
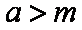
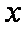
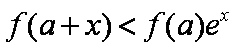
( 注意:对于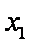
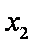
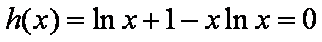
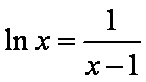
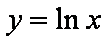
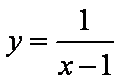
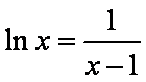
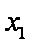
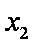
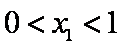
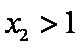
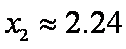
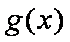
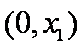
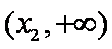
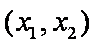
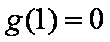
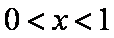
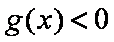
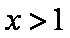
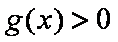
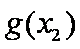
知识点
若函数





(1)已知函数


(2)记向量






(3)对于函数

正确答案
见解析
解析
(1)

依题意得

∴

(2)依题意,
将
得到函数
再将所得的图象上所有点向左平移

即
∵

∵


∴
………………10分
(3)若函数
则存在


令

因此


显然上式对任意的
所以函数
(注:本题若化成
知识点
小明打算从







(1)求小明选择
(2)设

正确答案
见解析
解析
(1)设小明选择



即

(2)依题意得

∴

知识点
已知函数

正确答案
m>1
解析
函数






知识点
如图,过圆O外一点P作该圆的两条割线PAB和PCD,分别交圆O于点A,B,C,D弦AD和BC交于Q点,割线PEF经过Q点交圆O于点E、F,点M在EF上,且
(1)求证:PA·PB=PM·PQ
(2)求证:
正确答案
见解析
解析
解析:(1)∵∠BAD=∠BMF,
所以A,Q,M,B四点共圆,……………3分
所以
(2)∵
∴
又 

∴

∵
∴

所以
知识点
已知函数
(1)若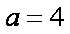
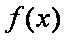
(2)设函数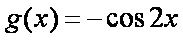
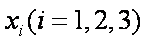
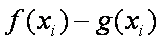
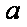
正确答案
见解析
解析
(1)由已知得
则当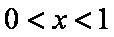
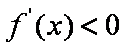
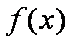
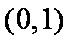
当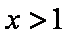
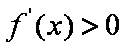
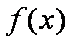
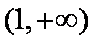
故函数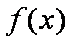
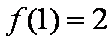
(2)若存在,设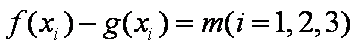
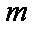
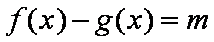
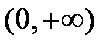
设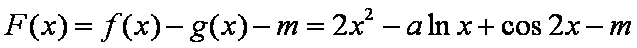
则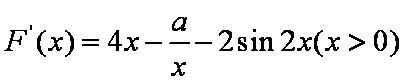
方法一: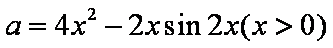
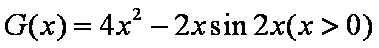
则
设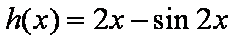
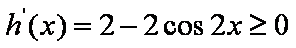
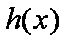
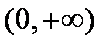
则当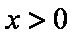
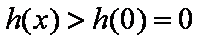
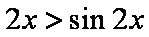
又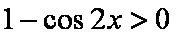
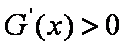
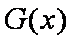
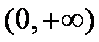
则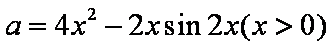
方法二:关于方程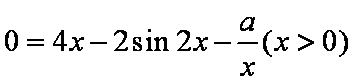
当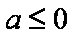
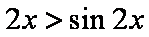
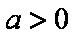
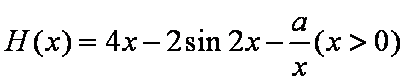
知识点
已知函数





(1)求函数
(2)若

正确答案
见解析
解析
解析:(1)
由

由
(2)由

又




知识点
已知函数
(1)若
(2) 若曲线




正确答案
见解析。
解析
(1)
又f(2)=ln3-1,f(4)=1+ln5,

(2)函数

所以曲线

因为切线与曲线有唯一的公共点,
所以方程

令
则
① 当a=1时,
② 当a
在区间

在区间
而
因此

即当
知识点
设函数


正确答案
解析

因为



从而有

知识点
如图,已知矩形






(1)求证:

(2)求二面角
正确答案
见解析
解析
解析:(1)建立如图所示的空间直角坐标系,
则



取



所以




……………………………………………6分
(2)由(1)知平面




所以向量





知识点
扫码查看完整答案与解析