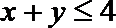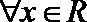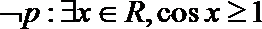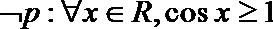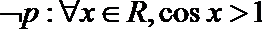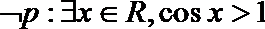- 命题的否定
- 共34题
5.下列有四个命题中，
①若
②已知O,A.B.C四点不共线，
③命题“
④若
正确的为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．给定两个命题
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4．命题 “如果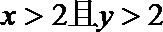
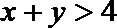
正确答案
如果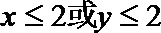
解析
解析已在路上飞奔，马上就到！
知识点
3．以下有关命题的说法错误的是（ ）
A命题“若
B“
C若
D对于命题
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．“a≤0”是“函数f（x）＝|（ax－1）x|在区间（0，＋∞）内单调递增”的（ ）
正确答案
解析
当a＝0时，f（x）＝|（ax－1）x|＝|x|在区间（0，＋∞）上单调递增；
当a＜0时，结合函数f（x）＝|（ax－1）x|＝|ax2－x|的图象知函数在（0，＋∞）上单调递增，如图（1）所示：
当a＞0时，结合函数f（x）＝|（ax－1）x|＝|ax
所以，要使函数f（x）＝|（ax－1）x|在（0，＋∞）上单调递增只需a≤0．
即“a≤0”是“函数f（x）＝|（ax－1）x|在（0，＋∞）上单调递增”的充要条件．
知识点
3．下列四种说法中，正确的是（ ）
A
B“若
C“命题
D命题“
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2． 下列说法错误的是（ ）
A若命题
B命题“若
C若y＝f（x）为偶函数, 则y＝f（x＋2 ）的图象关于直线
D“a=1”是“函数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
15．设{an}是等比数列，则“a1<a2<a3”是“数列{an}是递增数列”的 （ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
1.已知命题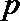 
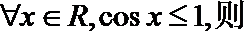
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3．已知命题P：∀x∈R，ex﹣x﹣1＞0，则￢P是（ ）
A∀x∈R，ex﹣x﹣1＜0
B∃x0∈R，
C∃x0∈R，
D∀x∈R，ex﹣x﹣1≤0
正确答案
解析
因为全称命题的否定是特称命题，所以，命题P：∀x∈R，ex﹣x﹣1＞0，则￢P是∃x0∈R，
考查方向
解题思路
直接利用全称命题的否定是特称命题写出结果即可。
易错点
本题是基础题目，要让学生记住命题否定的特点是“改变量词否定结论”。
知识点
扫码查看完整答案与解析