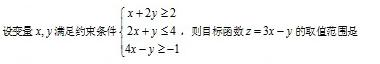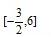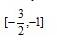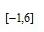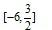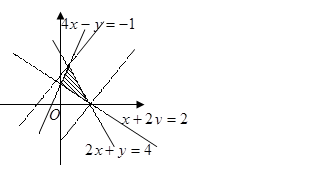相交弦所在直线的方程
共35题

· 相交弦所在直线的方程

相交弦所在直线的方程
共35题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知函数是定义在上的偶函数，且对任意的，都有.当时，.若直线与函数的图象在内恰有两个不同的公共点，则实数的值是

B0或

C或

D0或

正确答案

解析

略

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 4 分

在实数集R中，我们定义的大小关系“”为全体实数排了一个序，类似地，我们在复数集C上也可以定义一个称为“序”的关系，记为“”，定义如下：对于任意两个复数，当且仅当，下面命题①1i0;②若，，则；③若，则对于任意，；④对于复数，则其中真命题是

正确答案

①②③

解析

略

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 5 分

如图，是圆的直径，延长至，使，且，是圆的切线，切点为，连接，则（）；（）。

正确答案

，

解析

略

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 5 分

有下列命题：

①在函数的图象中，相邻两个对称中心的距离为；

②函数的图象关于点对称；

③关于的方程有且仅有一个实数根，则实数；

④已知命题：，都有，则是：，使得.

其中真命题的序号是_______.

正确答案

③④

解析

略

知识点

相交弦所在直线的方程

题型：单选题

单选题 · 5 分

正确答案

解析

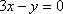
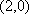
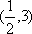
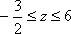
作出可行域，直线，将直线平移至点处有最大值，点处有最小值，即.答案应选A。

知识点

相交弦所在直线的方程

题型：简答题

简答题 · 14 分

如图，四棱锥中，平面平面,// ,,,且，.

（1）求证：平面；

（2）求和平面所成角的正弦值；

（3）在线段上是否存在一点使得平面平面，请说明理由。

正确答案

见解析

解析

（1）由，.,

可得。

由，且，

可得。

又。

所以，

又平面平面，

平面平面，

平面，

所以平面，　　　　　　　　　……………５分

（2）如图建立空间直角坐标系，

则，，，，

，，。

设是平面的一个法向量，则，，

即

令，则。

设直线与平面所成的角为，

则。

所以和平面所成的角的正弦值，　　　　　　……………1０分

（3）设，。

，，.

则。

设是平面一个法向量，则，，

即

令，则。

若平面平面，则，即，.

所以，在线段上存在一点使得平面平面.……………14分

知识点

相交弦所在直线的方程

题型：单选题

单选题 · 5 分

已知圆O的半径为1，PA，PB为该圆的两条切线，A，B为两切点，那么的最小值等于........................................................................( )

正确答案

解析

略

知识点

相交弦所在直线的方程

题型：简答题

简答题 · 18 分

已知函数对任意的恒有成立。

（1）当b=0时，记若在）上为增函数，求c的取值范围；

（2）证明：当时，成立；

（3）若对满足条件的任意实数b，c，不等式恒成立，求M的最小值。

正确答案

见解析

解析

（1）因为任意的恒有成立，

所以对任意的，即恒成立。

所以，从而.，即：。

当时，记（）

因为在上为增函数，所以任取，，

恒成立。

即任取，，成立，也就是成立。

所以，即的取值范围是。

（2）由（1）得，且，

所以，因此.

故当时，有.

即当时，.

（3）由（2）知，，

当时，有

设，则，

所以，由于的值域为，

因此当时，的取值范围是；

当时，由（1）知，.此时或0，，

从而恒成立。

综上所述，的最小值为

知识点

相交弦所在直线的方程

题型：单选题

单选题 · 5 分

下列函数中，对于任意，同时满足条件和的函数是（）

正确答案

解析

略

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 4 分

若圆的半径为1，圆心在第一象限，且与直线和轴相切，则该圆的标准方程是________.

正确答案

解析

略

知识点

相交弦所在直线的方程

继续学习学习下一知识点

下一知识点 : 直线和圆的方程的应用

百度题库 > 高考 > 理科数学 > 相交弦所在直线的方程

扫码查看完整答案与解析