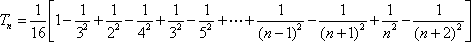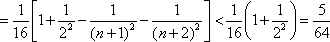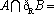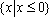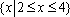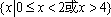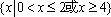- 直线和圆的方程的应用
- 共43题
请你谈一谈对“不同生产方式以及生产工艺中，生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
执行如图所示的程序框图，如果输出s＝3，那么判断框内应填入的条件是（ ）
正确答案
解析
由程序框图可知，输出的结果为s＝log23×log34×…×logk（k＋1）＝log2（k＋1），由s＝3，即log2（k＋1）＝3，解得k＝7.又∵不满足判断框内的条件时才能输出s，∴条件应为k≤7
知识点
正项数列{an}的前n项和Sn满足：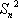
（1）求数列{an}的通项公式an；
（2）令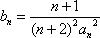
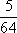
正确答案
见解析
解析
（1）解：由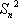
由于{an}是正项数列，所以Sn>0，Sn＝n2＋n.
于是a1＝S1＝2，n≥2时，an＝Sn－Sn－1＝n2＋n－（n－1）2－（n－1）＝2n.
综上，数列{an}的通项an＝2n.
（2）证明：由于an＝2n，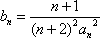
则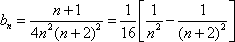
知识点
已知全集为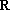
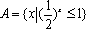
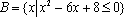
A
B
C
D
正确答案
解析
略
知识点
已知圆C1：（x－2）2＋（y－3）2＝1，圆C2：（x－3）2＋（y－4）2＝9，M，N分别是圆C1，C2上的动点，P为x轴上的动点，则|PM|＋|PN|的最小值为（ ）。
A
B
C
D
正确答案
解析
圆C1，C2的圆心分别为C1，C2，由题意知|PM|≥|PC1|－1，|PN|≥|PC2|－3，∴|PM|＋|PN|≥|PC1|＋|PC2|－4，故所求值为|PC1|＋|PC2|－4的最小值，又C1关于x轴对称的点为C3（2，－3），所以|PC1|＋|PC2|－4的最小值为|C3C2|－4＝
知识点
设{an}是有正数组成的等比数列，
A
B
C
D
正确答案
解析
由a2a4=1可得
知识点
设
正确答案
解析
约束条件对应四边形
知识点
不等式
正确答案
解析
知识点
设函数
（1）求
（2）讨论关于
正确答案
见解析。
解析
（1）
令
所以
（2）令
①当
在
②当
由①②得，函数
当
当
当
知识点
如图，在矩形区域ABCD的A，C两点处各有一个通信基站，假设其信号的覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源，基站工作正常)，若在该矩形区域内随机地选一地点，则该地点无信号的概率是( )。
A
B
C
D
正确答案
解析
S矩形ABCD＝1×2＝2，S扇形ADE＝S扇形CBF＝
P＝
知识点
扫码查看完整答案与解析