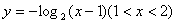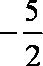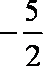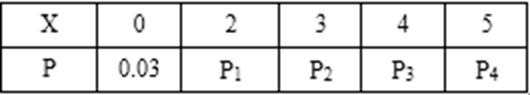相交弦所在直线的方程
共35题

· 相交弦所在直线的方程

相交弦所在直线的方程
共35题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 14 分

已知抛物线＝，圆的圆心为点M。

（1）求点M到抛物线的准线的距离；

（2）已知点P是抛物线上一点（异于原点），过点P作圆的两条切线，交抛物线于A，B两点，若过M，P两点的直线垂足于AB，求直线的方程。

正确答案

（1）（2）

解析

（1）解：由题意可知，抛物线的准线方程为：所以圆心M（0,4）到抛物线的距离是

（2）解：设P（x0, x02），A（）B（），由题意得设过点P的圆C2的切线方程为y-x0=k（x- x0）

即， ①

则

即

设PA，PB的斜率为，则是上述方程的两根，所以

，

将①代入得，

由于是此方程的根，故所以

由MP⊥AB,得，解得

即点P的坐标为，所以直线l的方程为

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 4 分

函数的反函数是

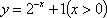
正确答案

解析

略

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 4 分

若关于x，y的线性方程组的增广矩阵为，该方程组的解为，则mn的值等

等于

正确答案

-24

解析

略

知识点

相交弦所在直线的方程

题型：填空题

填空题 · 4 分

13.的展开式中常数项为__________.

正确答案

解析

∵的通项为，令，∴，故展开式中常数项为

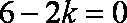
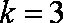
知识点

相交弦所在直线的方程

题型：简答题

简答题 · 12 分

18．某次飞镖比赛中，规定每人最多发射3镖．在M处每射中一镖得3分，在N处每射中一镖得2分，如果前两次得分之和超过3分即停止发射，否则发射第三镖．某选手在M处的命中率q1为0.25，在N处的命中率为q2，该选手选择先在M处发射第一镖，以后都在N处发射．用X表示该选手比赛结束后所得的总分，其分布列为：

（1）求随机变量X的数学期望E（X）；

（2）试比较该选手选择上述方式发射飞镖得分超过3分与选择都在N处发射飞镖得分超过3分的概率的大小．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相交弦所在直线的方程

继续学习学习下一知识点

下一知识点 : 直线和圆的方程的应用

百度题库 > 高考 > 理科数学 > 相交弦所在直线的方程

扫码查看完整答案与解析