- 点与圆的位置关系
- 共75题
13.在平面直角坐标系xOy中,点P是第一象限内曲线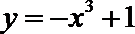
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知点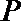
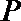
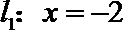
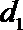
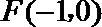
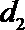
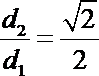
(1)求动点P所在曲线C的方程;
(2)直线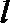
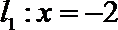
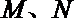
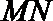
(3)记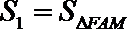
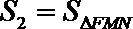
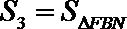
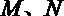
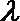
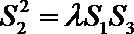
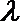
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知中心为







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,





(Ⅰ)若

(Ⅱ)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知△ABC的角A,B,C所对的边分别为a,b,c,且b是a,c平均数,则
正确答案
解析
根据题意,
所求数值是一个定值,
故可利用满足条件的特殊三角形进行计算.
若△ABC为等边三角形,
则A=B=C=60°,
所以
故选B.
知识点
20.已知函数
(1)求

(2)在





正确答案
所以,
所以,函数
(2)由
因为

由
两边平方,整理得,

所以
得

所以


所以,当

解析
解析已在路上飞奔,马上就到!
知识点
设







21.当


22.求过点



正确答案

解析
设M的坐标为






考查方向
解题思路
由相关点法求轨迹方程,
易错点
不能想到相关点法求轨迹方程,设而不求的思想即弦长公式利用。
正确答案

解析










考查方向
解题思路
由弦长公式求弦长。
易错点
不能想到相关点法求轨迹方程,设而不求的思想即弦长公式利用。
20.已知圆






(I)求
(II)若直线






正确答案
(I)
解析
试题分析:本题属于圆锥曲线中的圆、曲线方程的求法和直线与圆锥曲线的相关关系,第一题中主要考查结椭圆方程的掌握,要从中找出一些固定的量来确定轨迹的具体模型,从而求出曲线方程.第二问是存在性的问题,先假设存在满足条件的点,然后构造等量关系来确定是否存在,要用到“设而不求”的基本思想,构建合理的一元二次方程的模型
考查方向
本题考查了圆锥曲线中的圆、曲线方程的求法和直线与圆锥曲线的相关关系,通常与一元二次方程中的韦达定理综合考查.
解题思路
题考查了圆锥曲线中的圆、曲线方程的求法和直线与圆锥曲线的相关关系,解题步骤如下:
易错点
1、求轨迹方程时容易忽略
知识点
18.如图,阴影部分为古建筑物保护群所在地,其形状是以










(1)按下列要求建立函数关系:
①设



②设



(2)请你选用(1)中的一个函数关系,求

正确答案
(1)①

(2)
解析
试题分析:此类问题是典型的函数建模问题,难度较大。解决的关键是把实际问题转化为函数问题进行求解。
(1)①由题设知,在Rt△O1PT中,
∠OPT=


又OO1=1,所以OP
在Rt△OPQ中,

所以,Rt△OPQ的面积为

②由题设知,OQ= QT = t,O1T=1,且Rt△POQ∽Rt△PT O1,
所以

化简,得
所以,Rt△OPQ的面积为

(2)选用(1)中①的函数关系

由

列表
所以,当

(2)选

由

列表
所以,当

考查方向
本题主要考查直线、圆、解三角形等基础知识,考查学生的抽象概括能力、运算求解能力,建模能力,考查学生的数学应用意识.难度中等.
解题思路
本题主要考查直线、圆、解三角形等基础知识。
解题步骤如下:根据已知条件,合理建立函数关系式;利用导数求出函数的最值。
易错点
第一问不能正确读懂题意,因而无法下手;
第二问得出函数关系后,不知道用导数解决最值问题。
知识点
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析