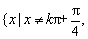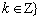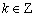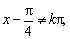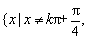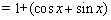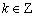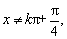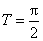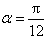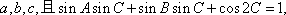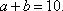- 二倍角的余弦
- 共45题
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:填空题
|
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
1
题型:填空题
|
函数

正确答案
p
解析
略
知识点
三角函数的周期性及其求法二倍角的余弦
1
题型:
单选题
|
若


正确答案
A
解析
因为


所以
知识点
三角函数中的恒等变换应用二倍角的余弦
1
题型:
单选题
|
函数
正确答案
C
解析
略
知识点
余弦函数的奇偶性余弦函数的单调性二倍角的余弦
1
题型:
单选题
|
函数
正确答案
D
解析
略
知识点
余弦函数的对称性二倍角的余弦
1
题型:简答题
|
已知函数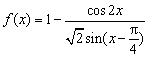
(1)求函数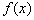
(2) 求函数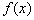
正确答案
(1)
(2) 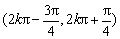
解析
(1)因为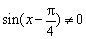
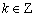
所以函数的定义域为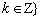
(2)因为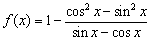
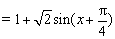
又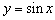
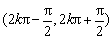
令 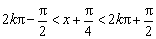
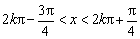
又注意到
所以
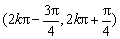
知识点
正弦函数的定义域和值域正弦函数的单调性两角和与差的正弦函数二倍角的余弦
1
题型:填空题
|
在




正确答案
解析
略
知识点
二倍角的余弦余弦定理
1
题型:简答题
|
已知函数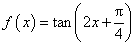
(1)求函数的定义域与最小正周期;
(2)设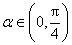
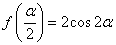
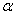
正确答案
(1)最小正周期为
(2)
解析
(1)函数的定义域满足
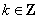
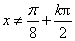
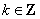
所以函数的定义域为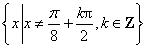
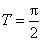
(2)解法1。 因为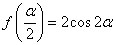
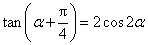
所以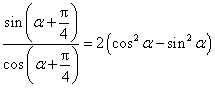
于是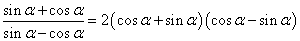
因为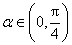
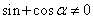
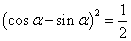
因而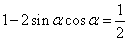
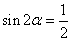
因为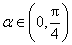
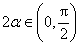
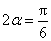
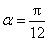
解法2。因为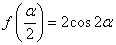
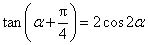
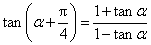
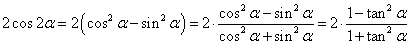
所以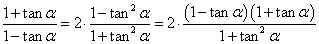
因为
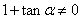
于是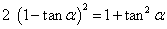
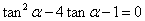
所以
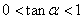
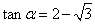
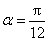
解法3。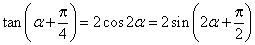

因为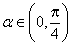
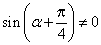
得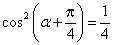
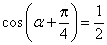
于是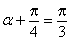
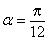
知识点
正切函数的定义域正切函数的周期性二倍角的余弦
1
题型:简答题
|
在△ABC中,角A,B,C的对边分别为
(1)求c的值;
(2)若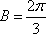
正确答案
见解析
解析
知识点
二倍角的余弦正弦定理余弦定理的应用
下一知识点 : 二倍角的正切
扫码查看完整答案与解析