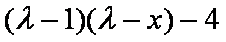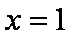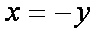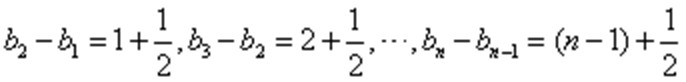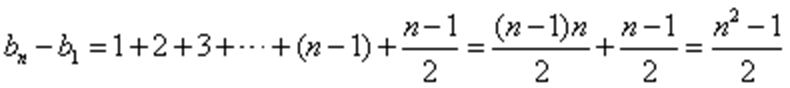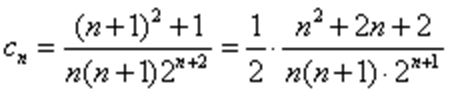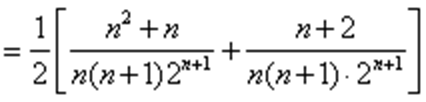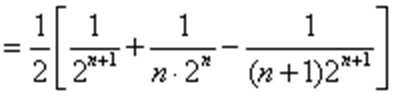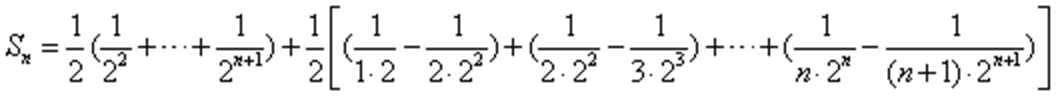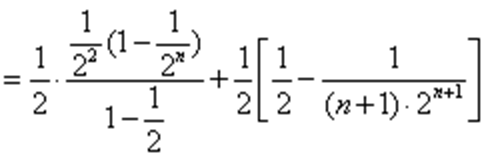- 数列
- 共2612题
已知正实数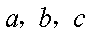
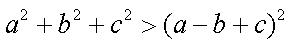
正确答案
见解析。
解析
因为正实数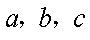
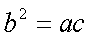
即有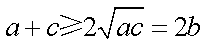
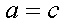
则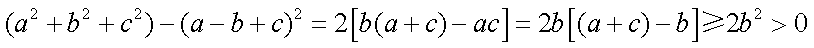
即证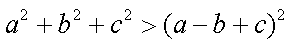
知识点
已知在等比数列



(1)求数列
(2)设数列





正确答案
见解析
解析
(1)设公比为




∴
(2)

两式相减得:
∴




两式相减得:
∴


记

∴
∴数列

故
知识点
已知

(1)若


(2)若数列


(ⅰ)数列
(ⅱ)
正确答案
见解析
解析
(1)
在


在


∴

(2)(ⅰ)用数学归纳法证明
当



令




而



于是,由


由数学归纳原理,
又由(1)知

∴

(ⅱ)我们先证明

令

在


而


故②成立,从而①成立。
由于

知识点
已知矩阵
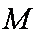
正确答案
见解析
解析
解:矩阵M的特征多项式为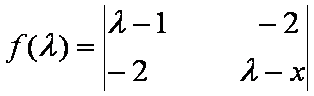
因为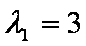
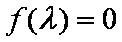
由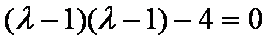
设
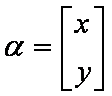
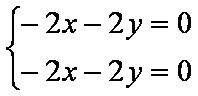
令
知识点
设


正确答案
见解析
解析
解:因为
同理
得
因为
知识点
已知矩阵


正确答案
见解析。
解析
设


解得

知识点
数列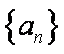
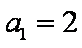
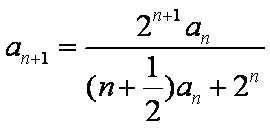

(1)设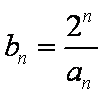
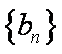
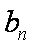
(2)设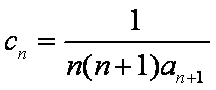
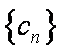
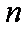
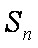
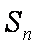
正确答案
见解析
解析
(1)由已知可得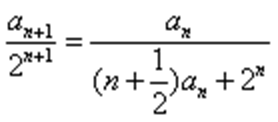
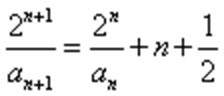
即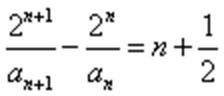
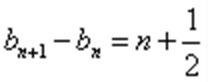
∴
累加得
又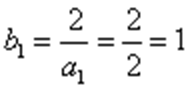
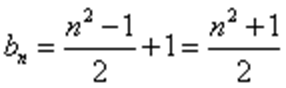
(2) 由(1)知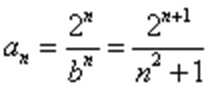
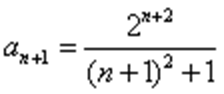
∴
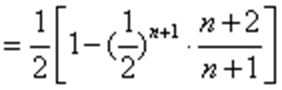
知识点
已知函数


(1)求实数
(2)已知结论:若函数








(3)已知正数





正确答案
见解析
解析
(1)



当



当







(2)令
则
函数




又
当



当



故对任意

(3)用数学归纳法证明。
①当









②假设当






则

…………13分


综上由①②,对任意

知识点
已知等比数列


(1) 求k的值及数列
(2) 若数列



正确答案
见解析。
解析
(1) 当



(2) 由





知识点
设等差数列


(1)若d=3,试判断
(2)证明:存在无穷多个d,使得对每一个m,
正确答案
见解析。
解析
(1)因为

假设



设



所以假设不成立,即
(2)证明:由题设知an=

由(1)知,要使对于一切m,
必须有:对于

即
当d=3k

故存在无穷多个d,满足对每一个m,
知识点
在等差数列
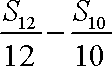
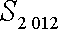
正确答案
解析
设公差为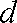
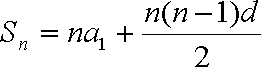
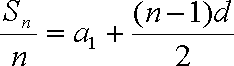
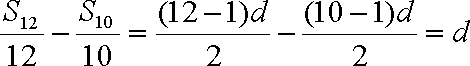
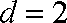
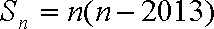
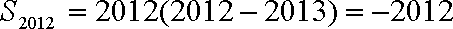
知识点
已知数列

(1)求证:

(2)求
正确答案
见解析。
解析
(1)当
假设当
则当

其中

所以
所以
(2)

知识点
已知等比数列





正确答案
见解析
解析
证明:由已知,得



(方法一)用数学归纳法证明。
①当


②假设当
那么当
所以当
综合①②,得
所以
(方法二)当


当
所以
知识点
求矩阵M=
正确答案
见解析。
解析
矩阵M的特征多项式为

令
当
所以矩阵M的属于特征值-1的一个特征向量为
当
所以矩阵M的属于特征值3的一个特征向量为
知识点
如右图所示,使电路接通,开关不同的开闭方式有
正确答案
解析
若前一个开关只接通一个,则后一个有



知识点
扫码查看完整答案与解析