- 数列
- 共2612题
在数列
(1)求数列

(2)若存在


正确答案
见解析
解析
解析:(1)
(2)

设

及


知识点
已知数列{an}首项a1=2,且对任意n∈N*,都有an+1=ban+c,其中b,c是常数。
(1)若数列{an}是等差数列,且c=2,求数列{an}的通项公式;
(2)若数列{an}是等比数列,且|b|<1,当从数列{an}中任意取出相邻的三项,按某种顺序排列成等差数列,求使{an}的前n项和
正确答案
见解析
解析
(1)当



因为




即



又









所以数列


(2)因为




即



当



当




则


所以有


解之得
又因为


由


因为


知识点
如图,过抛物线


(1)若△CBF,△CFA,△CBA的面积成等差数列,求直线l的方程;
(2)若

正确答案
见解析。
解析
(1)设直线

代入

设
则
又因为







即


所以所求直线方程为
(2)抛物线的焦点为

若

即
因为
又
且


得
若


若


由于

故(1)当


(2)当


即


(3)当


综上,

知识点
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程


③线性回归方程

④在一个
本题可以参考独立性检验临界值表
正确答案
解析
①③④正确,②回归方程


知识点
已知矩阵
(1)求逆矩阵
(2)若矩阵X满足
正确答案
见解析。
解析
(1)设




∴



(2)
知识点
已知

(1)求

(2)试比较

正确答案
见解析。
解析
(1)令


则

(2)要比较



当



当

猜想:当


由上述过程可知,
假设当

两边同乘以3 得:
而
即
∴当

综上得,当

当


知识点
已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项。
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意n∈N+均有
正确答案
见解析
解析
(1)由已知得



由于





又








(2)由



当



当




由 ①- ②得 












=1+2





知识点
设Sn为正项数列{an}的前n项和,且
(1)求数列{an}的通项公式;
(2)设

正确答案
见解析
解析
(1)解:∵
∴
两式相减可得

∴(an+an﹣1)(an﹣an﹣1﹣2)=0
∵{an}是正项数列,∴an﹣an﹣1=2(n≥2)
∵
∴a1=3
∴an=3+2(n﹣1)=2n+1;
(2)证明:∵

∴



∴Tn>2n
∵bn=


∴Tn=2n+2(



∴
知识点
已知正项等比数列{an}满足a7=a6+2a5,若存在两项am,an使得

正确答案
解析
试题分析:设正项等比数列{an}公比为

知识点
某医疗设备每台的销售利润与该设备的无故障使用时间










(1) 求
(2) 记

正确答案
见解析
解析
解析:(1)由已知得







(2)










随机变量


知识点
已知数列{

(1)令


(2)令



正确答案
(1)



解析
(1)在


当


又

于是
(2)由(1)得


由①-②得


于是确定

猜想:当
证法1:(1)当n=3时,由猜想显然成立。
(2)假设
则
所以当
综合(1)(2)可知 ,对一切
证法2:当
综上所述,当


知识点
已知正项等比数列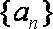
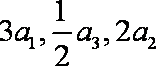
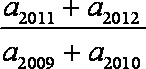
正确答案
解析
依题意,有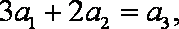
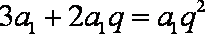
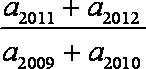
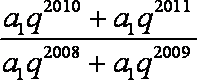
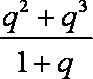
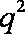
知识点
在等差数列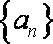
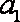
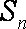

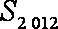
正确答案
解析
设公差为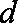
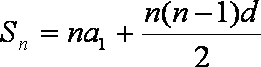
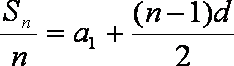
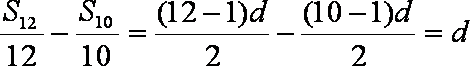
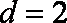
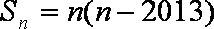
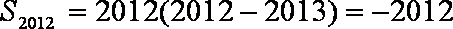
知识点
设等比数列{


正确答案
15
解析



知识点
设数列{






正确答案
解析
设公差为d,由





知识点
扫码查看完整答案与解析



































































