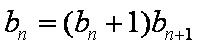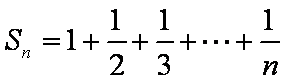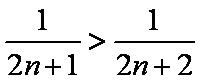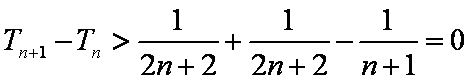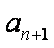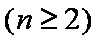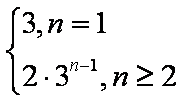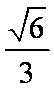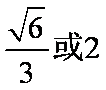- 数列
- 共2612题
已知前






(1)求数列
(2)是否存在正整数对


正确答案
见解析
解析
解析:(1)因为



设数列


将



于是


3分
(2)假设存在正整数对


当


3分
因为



故当且仅当


即当





故存在正整数对



知识点
已知数列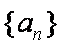
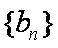
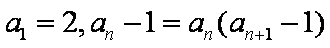
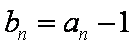
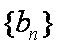
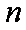
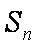
(1)求证:数列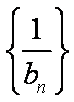
(2)设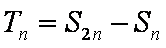
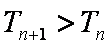
(3)求证:对任意的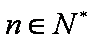
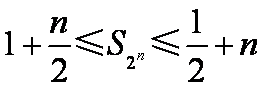
正确答案
见解析
解析
(1)证明:由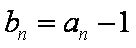
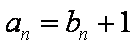
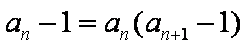
整理得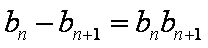
∵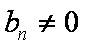
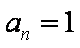
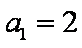
从而得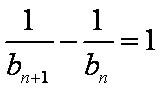
∵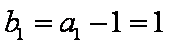
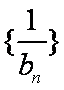
(2)∵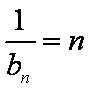
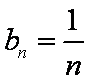
∴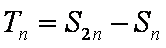
=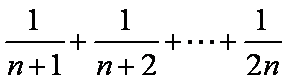
证法1:∵
=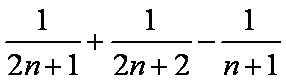
∴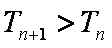
证法2:∵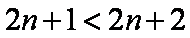
∴
∴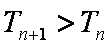
(3)用数学归纳法证明:
①当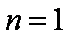

②假设当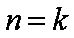
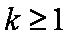
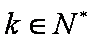
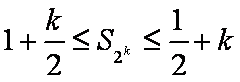
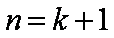
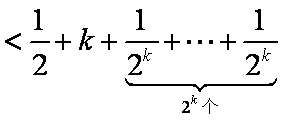
∴当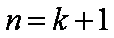
由①②知对任意的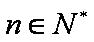
知识点
已知数列
(1)设


(2)求数列
(3)设
正确答案
见解析
解析
(1)




(2)设
3



(3)由已知得


∴ 存在


知识点
如右图所示,使电路接通,开关不同的开闭方式有
正确答案
解析
若前一个开关只接通一个,则后一个有



知识点
已知等比数列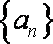
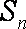
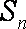
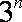
(1) 求k的值及数列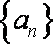
(2) 若数列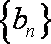
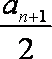
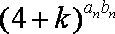
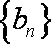
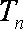
正确答案
见解析。
解析
(1) 当n≥2时由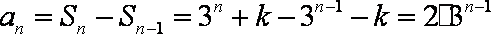
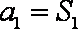
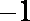
(2) 由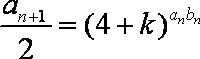
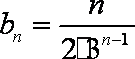
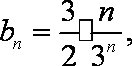
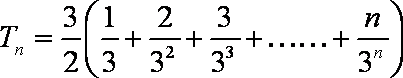
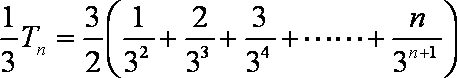
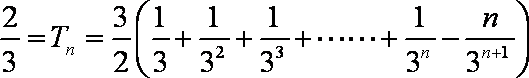
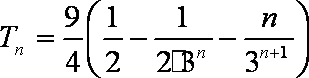
知识点
已知数列







(1)判断数列
(2)设

(3)对于(1)中数列















正确答案
见解析
解析
解析:(1)由题意得
又



(2)由(1)知

由



以上式子相加




则

(3)由(1)得

数列


当
当

又因为2011-1077=934=467
所以当

所以存在

知识点
将
正确答案
12
解析
先填第一行,则第一行有
知识点
已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项。
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意n∈N+均有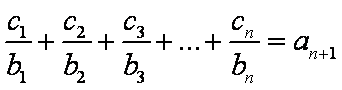
正确答案
见解析。
解析
(1)由已知得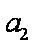
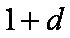
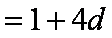
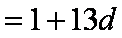
由于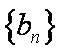
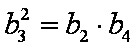
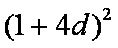
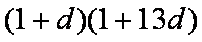
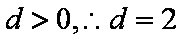
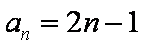
又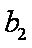
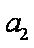
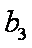
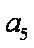
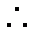
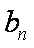
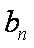
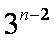
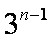
(2)由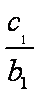
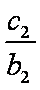
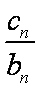
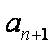
当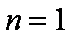
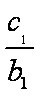
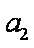
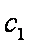
当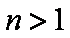
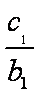
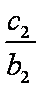
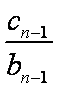
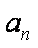
由①-②得 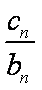
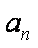
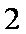
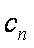
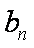
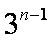
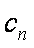
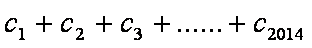
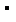
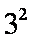
=1+2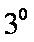
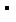
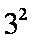
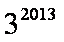
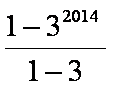
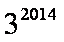
知识点
如图所示的数阵叫“莱布尼兹调和三角形”,他们是由正整数的倒数组成的,第




正确答案
解析
杨辉三角形中的每一个数都换成分数,就得到一个如图所示的分数三角形,即为莱布尼兹三角形。
∵杨晖三角形中第n(n≥3)行第3个数字是n
则“莱布尼兹调和三角形”第n(n≥3)行第3个数字是

知识点
已知数列{an}的前n项为和Sn,点(n,

(1)求数列{an}、{bn}的通项公式;
(2)设cn=

正确答案
见解析。
解析
(1)∵点(n,

∴
当n≥2时,an=Sn﹣Sn﹣1=
当n=1时,a1=S1=6,n+5=6,
∴
又bn+2﹣2bn+1+bn=0,
∴bn+2﹣bn+1=bn+1﹣bn,n∈N*,
∴{bn}为等差数列,
∵b1=5,∴
∴bn=b1+3(n﹣1)=3n+2,
∴
(2)证明:cn=
=
=
=
∴Tn=
=

∵Tn+1﹣Tn=

∴Tn单调递增,故(Tn)min=
∴Tn≥
知识点
在


正确答案
解析
因为






知识点
有限数列
① 对于任意的


② 对于任意的





(1)若





(2)证明:

(3)求
正确答案
见解析
解析
(1)由①,得
由②,当













经检验,当

(2)假设





由①,
对于数






所以 

(3)

(1)令

(2)设
(ⅰ)
假设






则对









同理:

但

所以 
所以 
(ⅱ)
假设
(ⅲ)
(ⅳ)
综合(ⅰ),(ⅱ),(ⅲ),(ⅳ)可知
………………14分
由(1),(2)可得,
知识点
在各项均为正数的等比数列






正确答案
解析
由



知识点
已知数列{




(I)求证数列{

(2)设


正确答案
见解析。
解析
(1)在


当


∴






于是

(2)∵

∴

由






知识点
已知实数1,m,9成等比数列,则圆锥曲线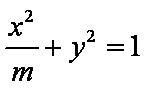
正确答案
解析
根据条件可知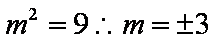
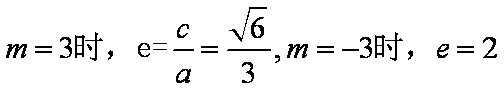
知识点
扫码查看完整答案与解析