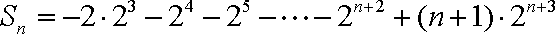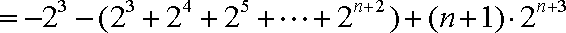数列_章节学习_百度题库

1

题型：单选题

|

单选题 · 5 分

若数列满足规律：，则称数列为余弦数列，现将1,2,3,4,5排列成一个余弦数列的排法种数为

A12

B14

C16

D18

正确答案

C

解析

①将3,4,5排在中间和两侧，再用1,2插两缝共种；

②将2,4,5排列，则结果必为21435；

将2,5,4排列，则结果必为21534；

将4,5,2排列，则结果必为43512；

将5,4,2排列，则结果必为53412. 故选C.

知识点

由数列的前几项求通项

1

题型：填空题

|

填空题 · 5 分

若等差数列{an}的前5项和=25，且，则

正确答案

7

解析

依题意，，则，∴

知识点

由数列的前几项求通项

1

题型：单选题

|

单选题 · 5 分

公差不为0的等差数列中, ,数列是等比数列，且,则（）

A4

B8

C16

D36

正确答案

D

解析

,即,,由知, ..

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

已知各项均不相同的等差数列的前四项和，且成等比数列.

（1）求数列的通项公式；

（2）设为数列的前n项和，求的值。

正确答案

（1）an=n+1（2）

解析

（1）设公差为d，由已知得 . …………3分

联立解得或（舍去）. …………5分

故. …………6分

（2） …………8分

…………10分

…………12分

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

设{}为等比数列，已知

（1）求数列的首项和公比；

（2）求数列的通项公式。

正确答案

见解析

解析

（1）设等比数列的公比为，则

∵

（2）解法一：由（I）知故

因此

解法二：设

由（1）

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

已知数列的前项和是，且。

（1）求数列的通项公式；

（2）设，求适合方程的正整数的值。

正确答案

见解析

解析

（1）当时，，由，得

当时，∵ ，

∴，即

∴

∴是以为首项，为公比的等比数列。

故　

（2），

解方程，得

知识点

由数列的前几项求通项

1

题型：单选题

|

单选题 · 5 分

已知等差数列的前次和为，且，则过点和（）的直线一个方向向量的坐标可以是（）

A（）

B（）

C（）

D（）

正确答案

B

解析

即 ∴ ∴ ∴;

∴，，，方向向量，故选（B）。

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 14 分

已知函数（为常数，且），且数列是首项为4，

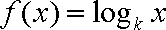
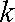
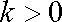
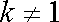
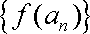
公差为2的等差数列.

（1）求证：数列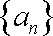是等比数列；

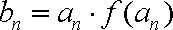
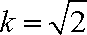
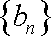
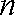
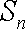
（2）若，当时，求数列的前项和；

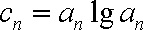
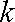
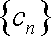
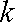
（3）若，问是否存在实数，使得中的每一项恒小于它后面的项？若存在，求出的范围；若不存在，说明理由。

正确答案

见解析

解析

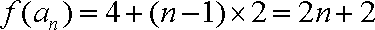
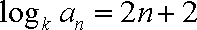
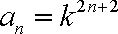
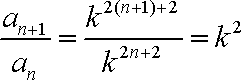
解析：（1）证：由题意，即， ……1分

∴∴. ……2分

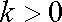
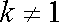
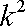
∵常数且，∴为非零常数，

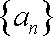
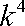
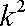
∴数列是以为首项，为公比的等比数列. ……3分

（2）解：由（1）知，，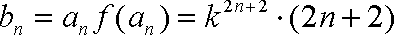

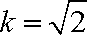
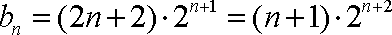
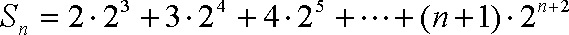
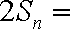
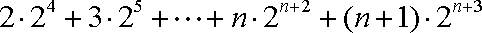
当时，. …………4分

∴， ①

. ② ……5分

②－①，得

∴ . ……8分

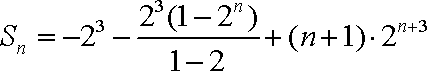
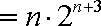
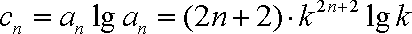
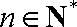
（3）解：由（1）知，，要使对一切成立，

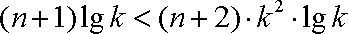
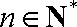
即对一切成立. ……9分

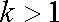
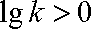
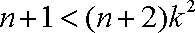
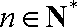
① 当时，，对一切恒成立；……10分

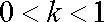
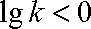
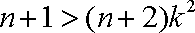
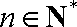
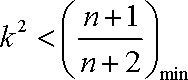
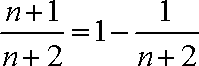
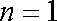
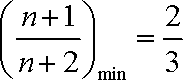
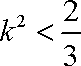
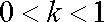
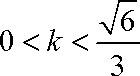
② 当时，，对一切恒成立，只需，……11分

∵单调递增，∴当时，. ……12分

∴，且， ∴. ……13分

综上所述，存在实数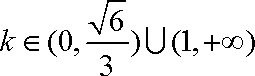满足条件. ……14分

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

已知为等差数列，且.

（1）求数列的通项公式；

（2）的前项和为，若成等比数列，求正整数的值

正确答案

见解析

解析

（1）设数列的公差为d，由题意得，

解得：

所以

（2）由（1）可得：

因成等比数列，所以

从而，即

解得：（舍去），因此.

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

若数列的前项和满足,等差数列满足.

（1）求数列、的通项公式;

（2）设,求数列的前项和为.

正确答案

见解析

解析

解析：（1）当时, ,∴

当时, , 即

∴数列是以为首项,3为公比的等比数列,∴ ， ……………4分

设的公差为

∴ ………………………6分

（2），

①

② ………………………8分

由①②得，

………………………12分

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

已知数列是一个公差大于0的等差数列，且满足，.

（1）求数列的通向公式；

（2）令，记数列的前项和为，对于任意的，不等式恒成立，求实数的最小值.

正确答案

（1）

（2）100

解析

（1）利用等差数列的性质求解；（2）利用裂项求和.

试题分析：（1）设等差数列的公差为，则依题设，

由得 ①

由得 ② (3分)

由①得将其代入②得，即，

∵，又，∴代入①得，

∴. (6分)

（2）由（1）得=

（9分）

由恒成立，则，

故m的最小值为100.（12分）

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

已知数列满足，.

（1）求数列的通项公式；

（2）若数列满足，求数列的通项公式。

正确答案

（1）（2）

解析

（1），，

而，故数列是首项为2，公比为2的等比数列，

，因此。 ( 5分)

（2）∵，∴，( 7分)

∴，

即，①

当时，，②

①－②得，，（10分）

可验证也满足此式，因此。（12分）

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

设数列满足:是整数,且是关于x的方程的根.

（1）若且n≥2时,求数列{an}的前100项和S100;

（2）若且求数列的通项公式.

正确答案

（1）598（2）

解析

解析：

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

已知数列的前项和是，且。

（1）求数列的通项公式；

（2）设，求适合方程的正整数的值.

正确答案

见解析

解析

（1）当时，，由，得

当时，∵ ，，

∴，即

∴

∴是以为首项，为公比的等比数列

故　

（2），

解方程，得

知识点

由数列的前几项求通项

1

题型：简答题

|

简答题 · 12 分

设正项等比数列的首项前n项和为，且

（1）求的通项；

（2）求的前n项.

正确答案

见解析

解析

（1）由得

即

可得　　

因为，所以解得，　　

因而　

（2）因为是首项、公比的等比数列，故

则数列的前n项和

前两式相减，得

即

知识点

由数列的前几项求通项

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点