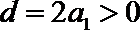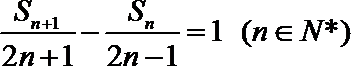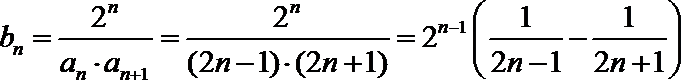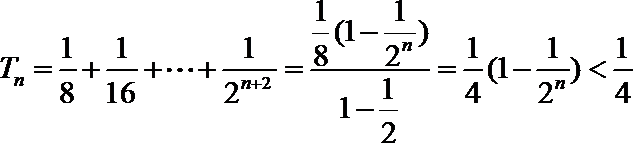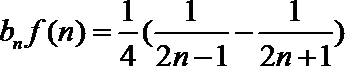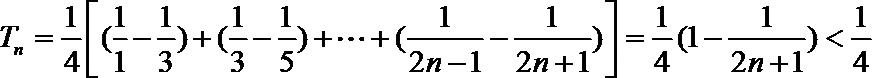- 数列
- 共2612题
3.在等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列
(Ⅰ)求数列
(Ⅱ)若



正确答案
解:(Ⅰ)


(1)-(2)得


又
解析
解析已在路上飞奔,马上就到!
知识点
12.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.数列






(I)分别求数列

(II)若对任意的


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.等差数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.单调递增数列



(1)求数列
(2)若数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.一列火车从重庆驶往北京,沿途有



(Ⅰ)求数列
(Ⅱ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.对于给定数列



(Ⅰ)已知数列{bn}是“M类数列”且bn=2n,求它对应的实常数p,q的值;
(Ⅱ)若数列{cn}满足c1=1,cn+1-cn=2n(n∈N*),求数列{cn}的通项公式.并判断{cn}是否为“M类数列”,说明理由.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.行列式

正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列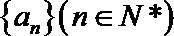
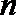
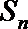
(1)当数列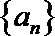
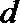
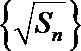
(2)若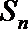
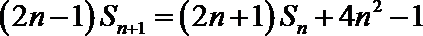
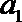
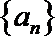
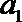
(3)若数列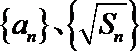
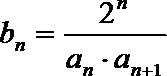
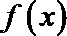
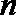
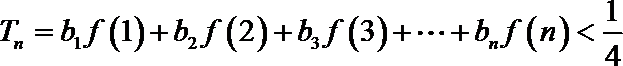
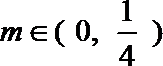
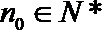
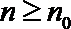
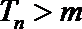
正确答案
(1)数列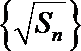
(2)∵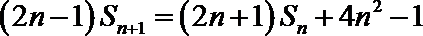
∴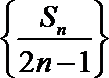
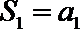
∴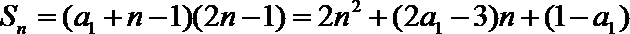
当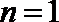
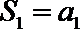
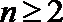
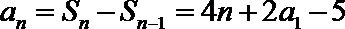
∵数列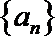
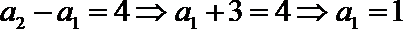
∴存在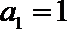
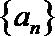
(3)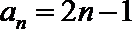
构造①:令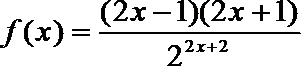
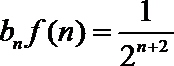
若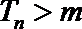
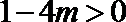
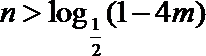
∴令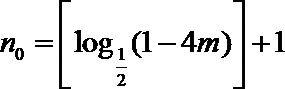
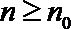
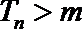
构造②:令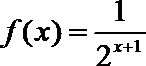
若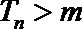
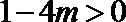
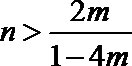
∴令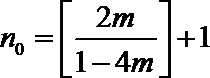
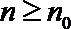
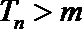
解析
解析已在路上飞奔,马上就到!
知识点
15.数列
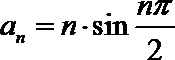


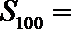
正确答案
-50
解析
解析已在路上飞奔,马上就到!
知识点
10.正项无穷等比数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.观察如图类似杨辉三角的数表,则此表最后一个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析