- 数列
- 共2612题
23．已知递增的等差数列
（1）求数列
（2）设数列
（3）若
正确答案
（1）∵
由 
∴
（2）∵
当
当
①－②得
∴
∴
（3）对于给定的
∵
即
即
∴对数列
使得
解析
解析已在路上飞奔，马上就到！
知识点
7．已知正项等比数列
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．若
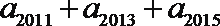
正确答案
122
解析
解析已在路上飞奔，马上就到！
知识点
17． 设数列
（1）求数列
（2）设
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．如果数列
A该数列的奇数项
B该数列的奇数项
C该数列的奇数项
D该数列的偶数项
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
23．若数列
（1）写出一个E数列
（2）若
（3）在
正确答案
解：（1）0，1，0，1，0是一具满足条件的E数列A5．
（答案不唯一，0，—1，0，1，0；0，±1，0，1，2；0，±1，0，—1，—2；0，±1，0，—1，
—2，0，±1，0，—1，0都是满足条件的E的数列A5）
（2）必要性：因为E数列A5是递增数列，
所以
所以A5是首项为12，公差为1的等差数列．
所以a2000=12+（2000—1）×1=2011．
充分性，由于a2000—a1000≤1，
a2000—a1000≤1
……
a2—a1≤1
所以a2000—at≤19999，即a2000≤a1+1999．
又因为a1=12，a2000=2011，
所以a2000=a1+1999．
故
综上，结论得证．
（3）对首项为4的E数列Ak，由于
……
……
所以
所以对任意的首项为4的E数列Am，若
则必有
又
所以n是最小值是9．
解析
解析已在路上飞奔，马上就到！
知识点
16．某学校高三年级共有学生200人，其中男生120人，女生80人．为了调查学生的学习状况，用分层抽样的方法从该校高三全体学生中抽取一个容量为25的样本，则应抽取女生的人数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．若
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．已知三个实数
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2． 若
正确答案
3
解析
解析已在路上飞奔，马上就到！
知识点
16．在等差数列
（Ⅰ）求
（Ⅱ）证明：
正确答案
（Ⅰ）设
因为
解得 
故
（Ⅱ）因为
所以
故
因为
所以
即
解析
解析已在路上飞奔，马上就到！
知识点
16．已知数列
（1）求数列
（2）设数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6．已知数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．无穷数列
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2．已知数列
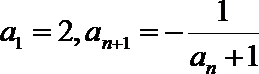
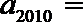
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
扫码查看完整答案与解析