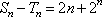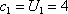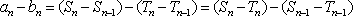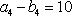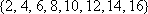- 数列
- 共2612题
在△ABC中,角A, B, C的对边分别为a, b, c,且A, B, C成等差数列。
(



(2)若

正确答案
(1)6(2)
解析
(1)
又

由


又由余弦定理得
∴

由①、②得,
(2)由(1)得


故



由



即


知识点
已知数列


(1)求

(2)设


正确答案
见解析。
解析
(1)设


解得

所以
(2)∵
∴
∴
知识点
定义:对于各项均为整数的数列











(1)

(2)




给出下面三个数列:
①数列


②数列
③数列
具有“

正确答案
解析
略
知识点
已知函数
(1)求
(2)若函数


(3)设各项为正的数列


正确答案
见解析。
解析
解析:(1)
令
当
当
∴
(2)①当

由(1)知


又当



∴

解得
②当

∴
所以原问题等价于
又
综上,实数a的取值范围是
(3)令


则
从而
即
知识点
已知数列







正确答案
1,
解析
略
知识点
把三阶行列式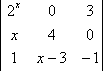
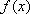

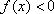
正确答案
解析
略
知识点
已知数列



正确答案
解析
略
知识点
设数列


①若

②若

③若



④若



正确答案
②③④
解析
略
知识点
已知等差数列数列





(1)求

(2)设




正确答案
见解析。
解析
(1)由已知可得





(2)由(1)知: 
∵






∵




知识点
设项数均为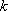
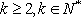
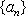
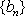
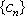

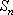
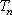
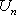
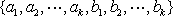
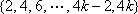
(1)已知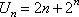
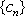
(2)若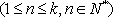
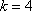
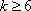
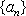
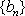
(3)若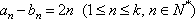
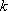
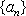
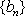
正确答案
见解析
解析
解析:(1)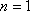
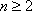
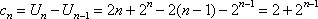
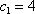
故,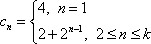
(2)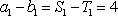
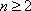
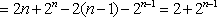
当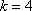
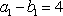
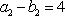
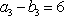
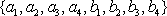
数列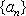
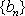
① 6,12,16,14;2,8,10,4 ② 16,10,8,14;12,6,2,4 …………………8分
当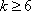
此时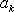
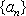
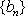
另证:
当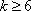
(3)令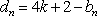
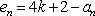
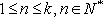
又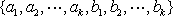
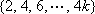
=
所以,数列对(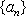
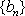
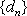
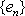
假设数列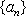
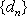
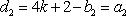
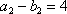
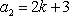
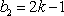
故,符合条件的数列对(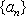
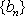
知识点
已知递增的等差数列




(1)求数列

(2)设数列



(3)若

正确答案
见解析
解析
。解析:1)∵






由 


∴
(2)∵


当


当


①-②得

∴
∴
(3)对于给定的


∵

即
即



∴对数列


使得
知识点
已知函数


(1)用n表示
(2)设

试比较

(3)设数列


正确答案
见解析,
解析
(1)
∴函数

令
(2)设数列






∴对于正整数n,当
当n=19时,
当
(3)证明:
要证
证法一:
∴原命题得证,
证法二:令

∴函数



∴原命题得证
证法三:
要证
只须证
以下用数学归纳法证明
①当n=1时,
②假设
则
∴当
根据①②可知列
知识点
已知数列




记

(1)求数列

(3)若

正确答案
见解析
解析
解析: 解:(1)


又

(2)由



∴数列




(3)因为
记

则
∴
由②-①得:
∴
知识点
已知数列





数列



数列



数列





(1)对于数列②,它的一个通项公式可以是
(2)求数列③的前

(3)在数列③中,若









正确答案
见解析
解析
(1)

(2)当

当

当


(3)由题意,


于是
把



由(1)(2)可得






于是可求得
故

或写成


知识点
数列{an}是以a为首项,q为公比的等比数列,令bn=1﹣a1﹣a2﹣…﹣an,cn=2﹣b1﹣b2﹣…﹣bn,n∈N*。
(1)试用a、q表示bn和cn;
(2)若a<0,q>0且q≠1,试比较cn与cn+1的大小;
(3)是否存在实数对(a,q),其中q≠1,使{cn}成等比数列,若存在,求出实数对(a,q)和{cn};若不存在,请说明理由。
正确答案
见解析。
解析
(1)当q=1时,bn=1﹣(a1+a2+…+an)=1﹣na,
当q≠1时,
=
=
所以
cn=
(2)因为
所以
当q>1时,1﹣q<0,1﹣qn+1<0;
当0<q<1时,1﹣q>0,1﹣qn+1>0,
所以当a<0,q>0且q≠1时,cn+1﹣cn<0,即cn+1<cn;
(3)因为q≠1,q≠0,
所以
因为{cn}为等比数列,则

所以


知识点
扫码查看完整答案与解析