- 数列
- 共2612题
14.已知等差数列{an}的公差d≠0,它的第1、5、17项顺次成等比数列,则这个等比数列的公比是__________.
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
4.已知各项不为





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设Sn是等差数列{an}的前n项和,若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.等比数列{an}中,a4=2,a5=5,则数列{lgan}的前8项和等于______
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列{an}的各项均是正数,其前n项和为Sn,满足( p-1) Sn=pn- an,其中p为正常数,且p≠1.
(1)求数列{an}的通项公式;
(2)设bn=

正确答案
(1)由题设知
解得a1=p.
由
两式作差得
所以
可见数列{an}是首项为p,公比为
(2)

解析
解析已在路上飞奔,马上就到!
知识点
5.将

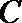
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.数列






(1)分别求数列

(2)设

正确答案
(1)由
得
①


(2)因为
所以
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
3.如果等差数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.观察下列等式:
照此规律, 第n个等式可为______________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列{an}中,a1=1,an+1=an+2n+1,且n∈N*。
(1)求数列{an}的通项公式;
(2)令bn= 
正确答案
(1)∵ an+1=an+2n+1,
∴ an―an-1=2n―1, 而 a1=1,
∴ an=a1+(a2―a1)+
(a3―a2)+……+(an―an-1)
=1+3+5+……+(2n―1)= 
(2) 由(1)知:
∴ 数列{bn}是递增数列,
∴ 最小值为

∴ m的取值范围是(
解析
解析已在路上飞奔,马上就到!
知识点
22.已知数列{an}的首项a1=5,前n项和为Sn,且n+1=2Sn+n+5, 且n∈N*。
(I)证明数列{an+1}是等比数列;
(II) 令f(x)=a1x+a2x2+……+anxn,求函数f(x)在点x=1处的导数f' (1),并比较2f' (1)与23n2―13n的大小.
正确答案
(I)
(II)由(I)知
因为
从而
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列





(Ⅰ)对任意实数

(Ⅱ)试判断数列
(Ⅲ)设







正确答案
(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即

所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1(
=

又b1x-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=(λ+18) ≠0,由上可知bn≠0,∴
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)·(-
Sn=-
要使a<Sn<b对任意正整数n成立,
即a<-


当n为正奇数时,1<f(n)
∴f(n)的最大值为f(1)=

于是,由①式得

当a<b

当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18)。
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


























































