- 数列
- 共2612题
4.已知公差不为0的等差数列{an}满足a1,a3,a4成等比数列,Sn为{an}的前n项和,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{an}的前n项和为Sn,且对任意正整数n,有Sn、an、n成等差数列.
(1)求证:数列{an+1}是等比数列,并求{an}的通项公式;
(2)求数列{
(3)数列{bn}满足b1=3, bn+1=λbn + an+1,若{bn}为等比数列,求实数λ.
正确答案
(1)依题意,
两式相减得,

(2)
(3)

解析
解析已在路上飞奔,马上就到!
知识点
14.已知













(Ⅰ)若

(Ⅱ)若

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
4.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知等比数列




正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
9.已知数列


正确答案
1或
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(Ⅰ)求证:数列

(Ⅱ)求数列


正确答案
(Ⅰ)







即

(Ⅱ)由(Ⅰ)知,即



设
则
①


又





解析
解析已在路上飞奔,马上就到!
知识点
5.已知等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知

正确答案
41
解析
解析已在路上飞奔,马上就到!
知识点
18.在数列
(1)求数列
(2)令

正确答案
(1)解:因为
所以
即
令
故

所以
因为

(2)因为
所以
所以

因为

解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列



(1)求证:数列
(2)求数列

正确答案
(1)∵

∵

∴
又
∴
∴数列


(2)由(1)得
∴

∴



将以上

∵
解析
解析已在路上飞奔,马上就到!
知识点
12.在等差数列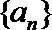
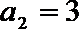
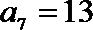
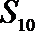
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.把4名中学生分别推荐到3所不同的大学去学习,每个大学至少收一名,全部分完,不同的分配方案数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知数列


数列


(Ⅰ)求

(Ⅱ)假设数列




正确答案
(Ⅰ)当
当
所以,
由
所以,

所以,
(Ⅱ)证明:当
当
故
综上,
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

















































